6. NumPy配列の基本

NumPyと呼ばれるライブラリの存在はPythonが広く科学技術計算に用いられるようになった最も大きな要因の一つであろう．ここでは科学技術計算で用いられる大規模データの効率的な扱いを可能にするNumPyの多次元配列オブジェクトについて学ぼう．なお，以降はこの多次元配列オブジェクトを便宜的にNumPy配列と呼ぶことにする．

参考

サンプルコード

6.1. NumPyについて

NumPy はPythonによる科学技術計算の根幹をなすライブラリである [1] ．このライブラリが提供する numpy というモジュールを使うためには

>>> import numpy as np

のようにするのが一般的である．これは numpy という名前のモジュールを import し， np という別名を付けることを意味する．別名は必ずしもつけなくてもいいし，その別名を np にする必然性は何もない．しかし，世の中のほとんどのコードがこの書き方を採用しているので，ここでも慣例に従っておこう．以降では常に np が numpy モジュールを意味するものとする．

NumPy配列(NumPyが提供する多次元配列オブジェクト)は正確には np.ndarray オブジェクトである [2]．一般にPythonはスクリプト言語に分類される動作の遅い言語であるが，NumPy配列を用いることで非常に高速な数値演算が可能となる．これはNumPy配列がCで実装されており，NumPy配列の演算は「うまく」使えばほとんどが内部的にはCのコードとして実行されるからである．詳細は以下で追々見ていくことにしよう．

6.2. 基本的な使い方

まずは基礎の基礎を抑えよう．例えば配列を作る最も簡単な方法の一つとして

>>> np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

のように np.arange() を使う方法がある．np.arange() の引数に配列の長さを指定することで連番の整数配列ができる．この例では10が指定されているので，長さ10の整数配列が生成されている．

次に \(0 < x < 2\pi\) の範囲を等間隔に \(N\) 分割し，その各点で \(\cos(x)\) を計算してみよう．

>>> N = 10
>>> x = np.arange(N)/N * 2*np.pi
>>> y = np.cos(x)

ここで整数の変数 N が配列のサイズである．2行目で配列 x を生成し，3行目でその配列の各要素について \(\cos(x)\) の値を計算している．

ここで2行目では np.arange() で生成した配列に対してスカラー値の掛け算や割り算(整数 / 整数 = 実数に注意)を実行していることが分かるだろう( np.pi は \(\pi\) の値である)．このとき，配列の各要素に対して演算がそれぞれ実行される．同様に3行目では配列の各要素に対して np.cos() 関数を呼び出し，結果として生成される新しい配列を y に代入している．このような使い方は Fortranの配列演算の使い方と全く同じ である．CやPythonの組み込みの配列 [4] では当然このような書き方は許されないが，NumPy配列はあたかもFortranの配列のように使えるのである．

このようにループを使わずに配列演算を記述できると確かに非常に便利であるが，NumPy配列の本当の利点は単に簡便さではなく，その演算速度にある．例えば y = np.cos(x) を(長さ N の配列 x および y が定義されているとして)Pythonのループを使って書くならば，

>>> for i in range(N):
>>>   y[i] = np.cos(x[i])

のようになるだろう [3] ．ここでNumPy配列の各要素へのアクセスにはCのように [] を使って行うことに注意しよう．計算自体は同じことだが，このループはPythonで実行されるため，その演算速度は配列演算を使った場合に比べて桁違いに遅い．これは配列演算は実質的にはCで書かれたNumPyライブラリ内で実行されることになるためである．すなわち，Python上で実行される処理は遅いのだが，Pythonから呼び出した関数がCやFortranで実装されていれば，その部分についてはCやFortranで高速に処理することができるのである．

Pythonは様々なことが手軽に実現できる非常に便利な言語であるが，ネックとなるのはその処理の遅さである．(したがって，何も考えずに書くといとも簡単に遅いコードが出来上がってしまう．）NumPy配列を使うことで重たい処理だけを他の言語で書かれた高速なライブラリに押し付けることができ，手軽さと計算速度の速さを両立しているわけである．したがって， Pythonではループ処理をするのは可能な限り避け，可能な限り配列演算を利用するのが鉄則 である．

6.3. 配列オブジェクト

NumPy配列オブジェクト np.ndarray は多次元配列データを格納し効率的な演算を実現する．

6.3.1. 属性

NumPy配列の場合は当然ながら各要素をデータとして持つが，それに加えて以下の属性が重要である．

属性	意味
dtype	配列要素のデータ型(整数，実数，複素数など)
ndim	次元数
size	配列サイズ（要素数)
shape	配列形状

以下の例を見てみよう． np.arange() で生成された配列 x について見てみると，これは64bitの整数( int64 )配列であり，次元数は1，は配列サイズは10である．最後の形状は各次元の長さをtupleで表したものであるが，この場合は1次元配列なので (10,) となっている．例えば3次元配列で各次元の長さが 3, 4, 5 だったとすると (3, 4, 5, ) がその配列の形状となる．

>>> x = np.arange(10)
>>> x.dtype
dtype('int64')
>>> x.ndim
1
>>> x.size
10
>>> x.shape
(10,)
>>> np.array([[1, 2, 3], [4, 5, 6]]).shape
(2, 3)

6.3.2. データ型

NumPy配列に格納されるデータ型( .dtype 属性)はほとんどの場合はCやFortranの組み込み型と同等のものである．以下に代表的なNumPyのデータ型とそれに対応するCやFortranのデータ型を示す．

NumPy	型コード	C	Fortran	備考
np.int32	'i4'	int32_t	integer(4) / integer	32ビット整数(通常はCの int ，NumPyの 'i' )
np.int64	'i8'	int64_t	integer(8)	64ビット整数(通常はCの long ，NumPyの 'l' )
np.uint32	'u4'	uint32_t		32ビット符号なし整数(通常はCの unsigned int )
np.uint64	'u8'	uint64_t		64ビット符号なし整数(通常はCの unsigned long )
np.float32	'f4'	float	real(4) / real	32ビット浮動小数点数(通常はNumPyの 'f' )
np.float64	'f8'	double	real(8)	64ビット浮動小数点数(通常はNumPyの 'd' ，Python組み込みの float )
np.complex64	'c8'	float complex	complex(4) / complex	実部・虚部が共に32ビット浮動小数点数の複素数
np.complex128	'c16'	double complex	complex(8)	実部・虚部が共に32ビット浮動小数点数の複素数(Python組み込みの complex )

少し古いデータ型の指定方法では一文字の型コードが使われていた．例えば

>>> np.dtype('d')
dtype('float64')
>>> np.dtype('i')
dtype('int32')

の例では 'd' は np.float64 ， i は np.int32 に対応している．しかし，これは環境に依存して変わってしまう可能性がある(例えば 'i' が 64ビット整数 np.int64 の環境もあってもおかしくはない）ので，NumPyでは明示的にデータサイズを示した np.int32 のような指定が推奨されている．

6.4. 生成

配列を生成するにはいくつかの方法があるが，以下に何もないところから配列を作るための典型的な例をいくつか示そう．

6.4.1. シーケンス型からの生成

既存のlistやtupleを np.array() 関数の引数に与えることでNumPy配列に変換することができる．使い方は以下の例を見れば明らかであろう．

>>> np.array([0, 1, 2, 3, 4])              # list [0, 1, 2, 3, 4] を変換
array([0, 1, 2, 3, 4])
>>> np.array((0, 1, 2))                    # tuple (0, 1, 2) を変換
array([0, 1, 2])
>>> np.array([[0, 1,], [2, 3], [4, 5]])    # listのlistを2次元配列に変換
array([[0, 1],
       [2, 3],
       [4, 5]])

6.4.2. arange

すでに見たように np.arange() は連番の配列を作る．いくつか別の使い方も見てみよう．

>>> np.arange(10, 20, 2)
array([10, 12, 14, 16, 18])

のように生成される配列の始点，終点，ステップを指定することもできる．指定の仕方は for ループでよく用いられる range() と同様である．また，

>>> np.arange(10, dtype=np.float64)
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

のように dtype を指定することで，生成される配列のデータ型を指定することもできる．

6.4.3. zeros

np.zeros() は0で初期化された配列を作るための関数である．以下の例

>>> np.zeros(10)
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

ではサイズが10の実数配列を生成している．デフォルトのデータ型が倍精度実数( np.float64 )であることに注意しよう．このデータ型は dtype オプションで指定することができる．

多次元の配列を生成するには，以下のように形状を指定すればよい．

>>> np.zeros((2, 4), dtype=np.int32)
array([[0, 0, 0, 0],
       [0, 0, 0, 0]], dtype=int32)

この例では形状として (2, 4) を指定しているので0で初期化された2次元配列ができている．

さらに np.zeros_like() を使うと，既に存在する別の配列と同じ形状・同じデータ型の配列を生成することもできる．

>>> x = np.zeros((3, 3), dtype=np.float32)
>>> np.zeros_like(x)
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]], dtype=float32)

6.4.4. ones

np.ones() は1で初期化する以外は np.zeros() と同じように使うことができる．例えば以下は2次元の配列を生成する．

>>> np.ones((3, 3))
array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])

ここでもデフォルトのデータ型が倍精度実数であることに注意しよう．

同様に np.ones_like() も np.zeros_like() の代わりに使うことができる．

>>> x = np.zeros((3, 3), dtype=np.float32)
>>> np.ones_like(x)
array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]], dtype=float32)

この例のように引数で与えられた配列の形状およびデータ型だけを受け継ぎ，その値は1で初期化されていることに注意しよう．

6.4.5. linspace

ある区間を均等に区切った点列を配列として作成したいときに便利なのが np.linspace() である．例えば \(0 \leq x \leq 1\) を均等に区切った配列を生成してみよう．

>>> np.linspace(0.0, 1.0, 11)
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])

ここで np.linspace() がデフォルトで端点(この場合は \(x = 0\) と \(x = 1\) )を含むことに注意しよう． \(x = 1\) を含まなくても良いのであれば np.arange() を用いて

>>> np.arange(10)/10
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])

としてもよい．

6.4.6. geomspace / logspace

np.linspace() によってある区間 \([a, b]\) を線形に均等に区切ることができた．同様に与えられた区間を対数スケールで等間隔に区切るために np.geomspace() と np.logspace() が提供されている．この両者の違いは np.geomspace() には区間の端点の値をそのまま引数として指定するのに対して， np.logspace() には \(\log_{10}(a)\) および \(\log_{10}(b)\) を引数として渡すことである．

>>> np.geomspace(0.1, 10.0, 11)  # [0.1,10]をlogで等間隔に区切る
array([ 0.1       ,  0.15848932,  0.25118864,  0.39810717,  0.63095734,
        1.        ,  1.58489319,  2.51188643,  3.98107171,  6.30957344,
       10.        ])
>>> np.logspace(-1, +1, 11)      # 全く同じ(log10(0.1) = -1, log10(10) = +1)
array([ 0.1       ,  0.15848932,  0.25118864,  0.39810717,  0.63095734,
        1.        ,  1.58489319,  2.51188643,  3.98107171,  6.30957344,
       10.        ])

上の2つの例は丸め誤差を除いて以下と全く同一の結果を与える．

>>> 10**np.linspace(np.log10(0.1), np.log10(10.0), 11)
array([ 0.1       ,  0.15848932,  0.25118864,  0.39810717,  0.63095734,
        1.        ,  1.58489319,  2.51188643,  3.98107171,  6.30957344,
       10.        ])

6.4.7. random

乱数配列を作るのも以下のように簡単にできる．

>>> np.random.random(5)               # [0, 1)の一様乱数(長さ5の配列)
array([0.80086594, 0.2513905 , 0.41056114, 0.14083936, 0.74182892])
>>> np.random.randint(0, 5, size=10)  # [0, 10)の整数乱数(長さ10の配列)
array([2, 4, 4, 3, 1, 0, 4, 2, 2, 1])
>>> np.random.random((3, 2))          # [0, 1)の一様乱数を形状(3, 2)の2次元配列として
array([[0.56945673, 0.5676268 ],
       [0.39896178, 0.0149435 ],
       [0.35165915, 0.93962764]])

なお，ここで np.random.random() というのは numpy モジュールの中の random モジュールの中の random() 関数という意味である．

6.5. 入出力

NumPyは配列の入出力用に便利な関数が用意されており，非常に簡単に使うことができる．

6.5.1. テキスト入出力

6.5.1.1. loadtxt

テキスト形式のデータファイルを読み込むには np.loadtxt() が大変便利である．ここではデータファイル helix1.dat を読み込んでみよう．このファイルの中身は以下のようになっており，値がスペースで区切られている．

 0.81  0.59  0.50
 0.31  0.95  1.00
(中略)
 0.81  0.59 15.50
 0.31  0.95 16.00

このファイルは以下のように1行で読み込むことができる．

>>> x = np.loadtxt('helix1.dat')
>>> x.shape
(32, 3)

読み込んだ結果は2次元配列として返される．この場合は32行 x 3列のデータのため .shape 属性は (32, 3) となっている． np.loadtxt() には多くのオプションがあるが，重要なものは以下の通りである．

パラメータ名	データ型	概要
dtype	np.dtype	デフォルトでは float ( np.float64 )
delimiter	str	値の区切り文字(デフォルトではスペース)
comments	str	各行のこの文字列に続く部分はコメントとみなされ無視する（デフォルトでは '#' )
skiprows	int	ファイル先端から指定された行数分だけ無視する（デフォルトでは0)

例えばスペースではなくカンマ , で区切られたいわゆるCSV(Comma-Separated Values)ファイルを読み込むには

>>> x = np.loadtxt('filename.csv', delimiter=',')

のように区切り文字を指定すればよい．

6.5.1.2. savetxt

np.loadtxt() の逆に配列をファイルに出力するには np.savetxt() を使えばよい．例えばNumPy配列オブジェクト x をoutput.datというファイルに出力するには

>>> np.savetxt('output.dat', x)

とすればよい． 代表的なオプションをいかにいくつか紹介しておこう．

パラメータ名	データ型	概要
fmt	str	フォーマット文字列
delimiter	str	値の区切り文字(デフォルトではスペース)
comments	str	ヘッダー・フッター用のコメント文字（デフォルトでは '#' )
header	str	ファイル先端のコメントヘッダー
footer	str	ファイル終端のコメントフッター

例えば helix1.dat を読み込み，同じフォーマットで別のファイルoutput.datに書き込むには

>>> x = np.loadtxt('helix1.dat')
>>> np.savetxt('output.dat', x, fmt='%5.2f')

のようにフォーマット文字列を指定すればよい．

6.5.2. バイナリ入出力

6.5.2.1. NPY形式とNPZ形式

単一のNumPy配列をバイナリのまま(メモリ上のバイト列をそのまま)ファイルに保存するファイル形式がNPY形式である．これはNumPyの独自フォーマットであるが，その形式は 公開 されている．さらに，複数のNumPy配列を単一のファイルに書き込む形式がNPZ形式である．まずはNumPy配列をこれらの形式で保存する例を見てみよう．NPY形式には np.save() ， またNPZ形式には np.savez() をそれぞれ用いる．例として，

>>> x = np.linspace(0.0, np.pi, 100)
>>> y = np.cos(x)

によって作成した配列を保存してみよう．

NPY形式で保存するには

>>> np.save('binary1.npy', x)

とすればよい．最初の引数がファイル名，2番目の引数が保存する配列である．また，NPZ形式で複数の配列を保存するには

>>> np.savez('binary1.npz', x_name=x, y_name=y)

のようにすればよい．ここで np.savez() には複数の配列を与えることになるため，それぞれに名前(この例では x_name および y_name )を与えていることに注意しよう．なお，ここではそれぞれ拡張子を .npy ， .npz としたファイル名を与えたが，そうでない場合には自動的にこれらの拡張子が付与される．

どちらの形式でもファイルを読み込むときには np.load() を用いればよい．NPY形式の場合は np.load() は読み込んだデータを直接NumPy配列として返すので，

>>> xx = np.load("binary1.npy")

のように使えばよい．ここでは xx に読み込まれた配列が代入される．NPZ形式の場合には np.load() はdict-likeなオブジェクトを返す．すなわち，

>>> data = np.load("binary2.npz")

のように読み込むと data はdictのように振る舞うオブジェクトが代入される．したがって，

>>> xx = data['x_name']
>>> yy = data['y_name']

によってそれぞれNumPy配列が得られる．ここで x_name や y_name は np.savez() に与えた配列の名前である．

6.5.2.2. 生のバイナリファイル

C言語の fwrite() 関数やFortranのストリーム出力で作成されたバイナリファイルは他の情報が何も付与されていない「生」のバイナリファイルである．このような生のバイナリファイルは np.fromfile() で読み込むことができる．基本的にはPython組み込みの open() 関数でファイルを開き， np.fromfile() でデータを読めばよい．

>>> # 読み込み専用(r)でファイルを開く
>>> fp = open('cbinary.dat', 'r')
>>> # np.float64のデータを10個読み込みNumPy配列としてzに代入
>>> z = np.fromfile(fp, np.float64, 10)
>>> # ファイルを閉じる
>>> fp.close()

生のバイナリファイルには余計な情報は一切付与されていないので，データの形式や個数をあらかじめ知っていなければ正しく読み込むことができないことに注意しよう．逆に言えば，それさえ理解してあれば自由自在にファイルを扱うことができる．基本的にファイルの操作は 公式ドキュメント に従って行えばよく，読み込んだバイト列をNumPy配列として評価したいときにだけ np.fromfile() を使えばよい．

6.5.2.3. unformatted形式(Fortran)

Fortranの unformatted形式 は，生のバイナリファイルに近いが，ヘッダとフッタが前後に付与されることが多い [8] ．ここでは scipy.io.FortranFile オブジェクトを用いた読み込み方法を紹介しておこう．

ここでは Fortran演習 で用いたunformatted形式のバイナリファイル helix2.dat を読み込んでみよう． FortranFile オブジェクトの read_record() メソッドはFortranの1回の write 文に対応するデータを読み込み，NumPy配列を返す．このファイルには3つの倍精度実数の配列が3回の write 文で保存されているので，

>>> from scipy.io import FortranFile
>>> # ファイルを開く
>>> fp = FortranFile('helix2.dat')
>>> # 3回のread_recordでそれぞれNumPy配列として読み込み
>>> x = fp.read_record(np.float64)
>>> y = fp.read_record(np.float64)
>>> z = fp.read_record(np.float64)
>>> # ファイルを閉じる．
>>> fp.close()

のように3回の read_record() メソッド呼び出しでそれぞれ読み込めばよい．倍精度実数データを読み込むので np.float64 を引数に与えていることに注意しよう．なお，1行目は scipy.io モジュールから FortranFile オブジェクトを読み込むことを意味する．

6.5.2.4. HDF5とnetCDF

バイナリファイルは高速に読み書きができ，またテキストへの変換がないため，情報が失われることが無いという利点がある．その一方で，可搬性に欠けるという欠点があり，ある計算機で生成したデータが他の計算機ではそのままでは読めないという問題が起こることがある．また，データ読み込みの際にはあらかじめ何が，どのような形式で書かれているかが分からなければデータの読み込みができない．このような欠点を補うファイルフォーマットとして比較的広く使われているのがHDF5である．C言語やFortranでHDF5を扱うのは少々面倒であるが，Pythonであれば h5py というモジュールを使うことで簡単に操作できる．

また同じような目的でnetCDFというデータ形式もあり，気象などの分野で使われているようである．最近のnetCDFは実は中身はHDF5で書かれているようなので，pythonであればやはりh5pyで操作が出来るし，netCDF専用のPythonモジュール( netcdf4-python )も存在する．

数値シミュレーションにはC/C++やFortranなどの高速な言語が用いられることが多いが，シミュレーションの結果をこれらの形式で出力しておけば，Pythonを用いた結果の解析が非常にやりやすくなるのである．

6.6. 各種演算

6.6.1. 算術演算

以下の例を見れば一目瞭然であろう．基本的にFortranの配列と同様な演算ができると思ってよい．

>>> a = np.arange(4)
>>> b = np.arange(4) + 4
>>> a + b
array([ 4,  6,  8, 10])
>>> a - b
array([-4, -4, -4, -4])
>>> a * b
array([ 0,  5, 12, 21])
>>> a / b
array([0.        , 0.2       , 0.33333333, 0.42857143])
>>> a**2
array([0, 1, 4, 9])

6.6.2. ユニバーサル関数

NumPy配列を引数にとり各要素にそれぞれ適用される関数は，NumPyではユニバーサル関数( ufunc )と呼ばれている(通常の関数と同じものだと考えてよい)．よく使うであろう数学関数は全て提供されていると考えてよい [5] ．Fortranなどでは提供されていない関数の使用例をいくつか示しておこう．なお，以下の例はスカラーに対して関数を呼び出しているが，配列を引数に与えた場合には各要素に対して演算した結果を返す．

>>> np.deg2rad(90.0)       # degreeからradianへの変換
1.5707963267948966
>>> np.rad2deg(np.pi/2)    # radianからdegreeへの変換
90.0
>>> np.lcm(4, 6)           # 最小公倍数
12
>>> np.gcd(12, 20)         # 最大公約数
4
>>> np.angle(1.0 + 1.0j)   # 複素数の偏角
0.7853981633974483

詳細は 公式ドキュメント を参照のこと．

6.6.3. メソッド

NumPy配列も当然オブジェクトなのでメソッドを持つ．また，多くのメソッドにはそれと対応する関数が存在する．以下で例を見てみよう．

配列の総和を計算するには np.sum() という関数を用いることができる．

>>> x = np.arange(10)
>>> np.sum(x)
45

これと同じことを配列 x のメソッド sum() を使って

>>> x.sum()
45

と表現することもできる．このように関数とメソッドがどちらも用意されているときにはどちらを使っても全く同じである．(メソッドの方が少しタイプ量が少ないし，タブキーでの補完を考えた時にはよいかもしれない．) 以下にもう少し例を示しておこう．

>>> x.max()   # 最大値
9
>>> x.min()   # 最小値
0
>>> x.mean()  # 平均値
4.5

単なる数値的な演算に限らず多くの便利なメソッドが用意されている．詳細は 公式ドキュメント を参照のこと．

6.7. インデックス操作

NumPyのインデックス操作は基本的にFortranの配列操作と似ているのでFortranユーザーには馴染みやすいだろう．

>>> x = np.arange(10)
>>> x[2]                 # 3番目の要素
2
>>> x[2:5]               # 3, 4, 5番目の要素(結果もNumPy配列)
array([2, 3, 4])
>>> x[:8:2] = -1         # 0, 2, 4, 6番目の要素に-1を代入
>>> x                    # 確認
array([-1,  1, -1,  3, -1,  5, -1,  7,  8,  9])
>>> x[::-1]              # 順番を反転
array([ 9,  8,  7, -1,  5, -1,  3, -1,  1, -1])
>>> x[-1]                # 最後の要素
9
>>> x[-2]                # 最後から2番目の要素
8

Fortranとの違いは負のインデックスを指定すると後ろから順に数えた要素を返すところである．実はこのようなインデックス操作はPython組み込みのシーケンス型(listなど)に対して行うこともできる．NumPy配列はこのインデックス操作をさらに強力なものにする．例えば，以下のようにインデックスを配列で渡すことも可能である．

>>> i = np.arange(1, 10, 2) # インデックス配列を作成
>>> i                       # 確認
array([1, 3, 5, 7, 9])
>>> x[i] *= 2               # 2倍にする
>>> x                       # 確認
array([-1,  2, -1,  6, -1, 10, -1, 14,  8, 18])
>>> x[i-1]                  # インデックスを一つずらす
array([-1, -1, -1, -1,  8])

のように使うことができる．(これは差分法に使うときなどに便利である．)

さらに，多次元配列のインデックス操作についても例を見てみよう．

>>> y = np.arange(20).reshape((4, 5)) # 長さ20の配列をreshapeで2次元配列に変換
>>> y
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
>>> y[0,:]                            # 1次元目は0，2次元目は全て
array([0, 1, 2, 3, 4])
>>> y[:,1]                            # 1次元目は全て，2次元目は1
array([ 1,  6, 11, 16])
>>> y[1:3,1:3]                        # 両次元とも1, 2番目の要素
array([[ 6,  7],
       [11, 12]])

より高次元の配列を扱う際には ... が便利である [6] ．

>>> z = np.arange(18).reshape((2, 3, 3)) # 3次元配列
>>> z
array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8]],

       [[ 9, 10, 11],
        [12, 13, 14],
        [15, 16, 17]]])
>>> z[...,0]                             # z[:,:,0]と同じ
array([[ 0,  3,  6],
       [ 9, 12, 15]])
>>> z[1,...,0]                           # z[1,:,0]と同じ
array([ 9, 12, 15])
>>> z[1]                                 # z[1,:,:]と同じ
array([[ 9, 10, 11],
       [12, 13, 14],
       [15, 16, 17]])

他にも色々と便利なのだがあまりにも機能が沢山あるので，これ以上は 公式ドキュメント を参照して欲しい．一つだけ配列の代入について注意しておこう．

>>> x[:] = 10 # 配列の全要素に10を代入
>>> x         # 確認
array([10, 10, 10, 10, 10, 10, 10, 10, 10, 10])
>>> x = 10    # 整数10をxに代入
>>> x         # xはスカラー
10

このように1行目と4行目では動作が異なる．Fortranでは4行目のように記述しても配列の全要素に10を代入してくれるが，Pythonでは 新しい変数を作り，そこに整数10を代入 する．これは動的型付け言語のPythonならではの動作である．配列の全要素にスカラー値を代入する際にはインデックスに : (もしくは ... )を指定しなければならない．

6.8. 形状操作

配列の形状は決して固定のものではない．実はこれまでの例にも既に出てきたが，

>>> x = np.arange(10)
>>> y = x.reshape((2, 5))
>>> x
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> y
array([[0, 1, 2, 3, 4],
       [5, 6, 7, 8, 9]])

のように reshape() メソッドによって配列の形状を変更することができる．この例ではまず長さ10の1次元配列 x を作って，それを形状(2, 5)の2次元配列 y に変換している．一体何が起こっているのだろうか？試しに y の要素を変更してみよう．

>>> y[1,0] = -1
>>> x
array([ 0,  1,  2,  3,  4, -1,  6,  7,  8,  9])
>>> y
array([[ 0,  1,  2,  3,  4],
       [-1,  6,  7,  8,  9]])

ここで変更したのはあくまで y の一つの要素であるが，それに伴って x の要素も変更されていることに注意しよう．すなわち， x も y もある連続したメモリブロック(この場合は8 byte x 10個 = 80 byte)への参照でしかない(つまりデータの実態は同じもの) [7] ． y に対しては2つのインデックスを使って要素を指定するが，これはあくまで人間から見た時の考えやすさのためにそうしてるに過ぎない．(これは何もPythonに限ったことでなく，Fortranでも同じことである．Cの場合は少し事情が複雑だが，staticな配列に限定すればやはり同じである．)

したがって，当然ながら reshape() 前後で要素数が同じである必要がある．試しに x を形状(3, 5)に変換しようとしても

>>> np.arange(10).reshape((3, 5))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: cannot reshape array of size 10 into shape (3,5)

のようにエラーとなる．

多次元配列の連続したメモリブロックを新たな1次元配列として得るために ravel() メソッドを使うことができる．似たようなメソッドとして flatten() があるが，これらの違いはなんだろうか．

>>> a = y.ravel()
>>> b = y.flatten()
>>> a
array([ 0,  1,  2,  3,  4, -1,  6,  7,  8,  9])
>>> b
array([ 0,  1,  2,  3,  4, -1,  6,  7,  8,  9])

見た目ではどちらも同じように見える．ここで y の要素を再び変更してみよう．

>>> y[1,0] = 5
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b
array([ 0,  1,  2,  3,  4, -1,  6,  7,  8,  9])

このように ravel() で作られた a は同じメモリブロックを参照しているのに対して， flatten() で作られた b は異なる領域を指していることが分かる．すなわち flatten() は新たなメモリブロックを確保し，データをコピーする．一方で， ravel() は単なる参照でしかない．当然 ravel() はデータをコピーする手間がない分高速に動作することに注意しよう．

なお，ここで紹介した形状操作はあくまでも初級編である．NumPyの演算速度を最大限に活かそうと思うと，このような配列形状の変更には思いのほか頻繁に出くわすことになるので少しずつ慣れていこう．

6.9. 第6章 演習課題

注釈

以下の課題はJupyter Notebookの使用を前提としているが，もちろん他の実行環境でも同等の処理を実現出来ていれば問題ない．ただし，この章の目的はNumPy配列の使い方の習得なので，以下の課題では 可能な限りループを使わず NumPyの機能を活かした実装を目指そう．

なお，以下では

>>> import numpy as np
>>> from matplotlib import pylab as plt

のように必要なモジュールが import されているものとする．

参考

解答例

6.9.1. 課題1

サンプルを実行して動作を確認せよ．

6.9.2. 課題2

整数 N を引数として受け取り， \(0^{\circ} \leq \theta \leq 180^{\circ}\) をN分割した点(端点を含むのでN+1点)，およびそれらの点における \(\sin \theta\) ， \(\cos \theta\) の値をそれぞれ配列として返す関数

def trigonometric(n):
    "θ, sinθ, cosθの値を出力する"
    pass

を作成せよ．これを呼び出し，例えば以下のようにプロットして結果を確認しよう．

>>> x, y1, y2 = trigonometric(18)
>>> plt.plot(x, y1, 'ro')
>>> plt.plot(x, y2, 'bo')
>>> plt.plot(x, np.sin(np.deg2rad(x)), 'r-')
>>> plt.plot(x, np.cos(np.deg2rad(x)), 'b-')

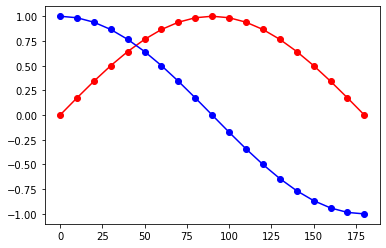
課題2

6.9.3. 課題3

以下の級数展開

\[e \simeq \sum_{n=0}^{N} \frac{1}{n !}. \quad (0! = 1に注意せよ)\]

により自然対数の底 \(e\) の近似値を求める関数 approx_e()

def approx_e(n):
    "自然対数の底を級数展開を用いて求める"
    pass

を作成しよう．ただし整数 N を引数として受け取り，内部ではNumPy配列を使うことでループを用いない実装とせよ．

ここで，階乗とガンマ関数の関係式

\[\Gamma(n) = (n-1)!\]

を用いてよい．ガンマ関数は scipy.special.gamma() を用いればよい．以下はその使用例である．

>>> from scipy import special
>>> special.gamma(3)  # 2!
2.0
>>> special.gamma(4)  # 3!
6.0

この関数を用いると例えば以下のような結果が得られる．

>>> print('{:20} : {:>20.14e}'.format('Approximated', approx_e(10)))
>>> print('{:20} : {:>20.14e}'.format('Exact', np.e))
Approximated         : 2.71828152557319e+00
Exact                : 2.71828182845905e+00

6.9.4. 課題4

以下の漸化式

\[p_{n+1} = p_n + \alpha p_n (1 - p_n)\]

で定義される数列 \(p_n (n=0, 1, \ldots)\) を考える．\(1 < \alpha < 3\) を \(m\) 分割し，各 \(\alpha\) について初期値 \(p_0 = 0.9\) から数列を生成し，そのうち \(n=100, \ldots, 200\) を \(\alpha\) の関数としてプロットしよう．

これには，整数 m を引数にとり，\(\alpha\) と \(p_n (n=100, \ldots, 200)\) の組を返す関数 logistic()

def logistic(m):
    "0 < α < 1 をm分割して，それぞれに対してロジスティック写像を計算"
    pass

を作成し，この関数を用いて

>>> a, p = logistic(2000)
>>> plt.scatter(a, p, s=0.001, color='r')
>>> plt.xlim(1.0, 3.0)
>>> plt.ylim(0.0, 1.4)

とすればよい．結果は以下の通りである．

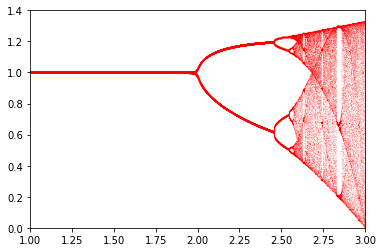
課題4

このような写像はロジスティック写像と呼ばれ，非常に単純な式ながら一定の条件を満たすときにはカオスを生み出すことが知られている．

6.9.5. 課題5

参考

アルゴリズムについては こちら を参照．

以下の積分

\[\int_{0}^{1} \frac{4}{\pi} \frac{1}{1 + x^2} dx\]

を台形公式およびSimpsonの公式を使って求める関数をそれぞれ作成しよう．ここで作成する関数は分割数 n を引数にとり，

def trapezoid(n):
    "分割数nの台形公式で関数を積分"
    pass

def simpson(n):
    "分割数nのSimpson公式で関数を積分"
    pass

のような形になるものとする．ただし関数内ではループを使わずに実装すること．これらの積分公式の誤差の分割数依存性は次のようにすれば調べることができる．

>>> M = 16
>>> n = 2**(np.arange(M)+1)
>>> err1 = np.zeros(M, dtype=np.float64)
>>> err2 = np.zeros(M, dtype=np.float64)
>>>
>>> for i in range(M):
>>>     err1[i] = np.abs(trapezoid(n[i]) - 1)
>>>     err2[i] = np.abs(simpson(n[i]) - 1)
>>>
>>> # 結果をプロット
>>> plt.plot(n, err1, 'rx-', label='trapezoid')
>>> plt.plot(n, err2, 'bx-', label='simpson')
>>> plt.loglog()
>>> plt.legend()

これによって得られる図は以下の通りである．

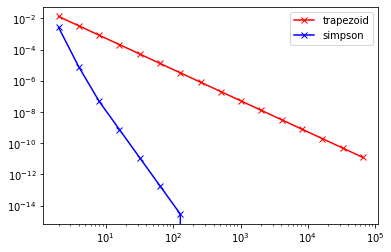
課題5

6.9.6. 課題6

データファイルに格納されている学生のテスト点数リストから，最高点，最大点，平均点，標準偏差を求めて返す関数 analyze_score() を作成しよう．ただし，

def analyze_score(filename):
    "filenameからデータを読んで最高点，最低点，平均点，標準偏差を返す"
    pass

のようにファイル名を引数にとるものとする．ここで，それぞれ対応する関数( np.max() ， np.min() ， np.mean() ， np.std() )またはNumPy配列のメソッドを用いること．

なお，データファイルは score1.dat および score2.dat とし，以下のようにこのファイルの最初の行にはデータ数，次の行は空行，以降に実際のデータが格納されている．

$ cat score1.dat
30      # データ数
        # 空白行
20      # 実際のデータはこれ以降の行
49
45
(以下略）

したがって， np.loadtxt() のオプション skiprows を用いて最初の2行を無視して読み込めばよい．

例えばscore1.datを読み込んだ場合には以下のような結果が得られる．

>>> smax, smin, savg, sstd = analyze_score('score1.dat')
>>>
>>> print('{:20} : {:10}'.format('Best', smax))
>>> print('{:20} : {:10}'.format('Worst', smin))
>>> print('{:20} : {:10.3f}'.format('Average', savg))
>>> print('{:20} : {:10.3f}'.format('Standard deviation', sstd))
Best                 :         98
Worst                :          6
Average              :     46.400
Standard deviation   :     25.115

同様にscore2.datについても試してみること．

6.9.7. 課題7

前問のscore1.datおよびscore2.datのようなデータファイルを読み込みヒストグラムを作成する関数 hist_score()

def hist_score(filename, nbin):
    "filenameからデータを読んでヒストグラムを作成する"
    pass

を作成しよう．ここで引数 nbin はビンの数である．関数 np.histogram() を用いること．

実行例は以下のようになる．

>>> nbin = 20
>>> bins, hist = hist_score('score2.dat', nbin)
>>> binw = bins[+1:] - bins[:-1]
>>> plt.bar(bins[0:-1], hist, width=binw, align='edge')
>>> plt.xlim(0, 100)

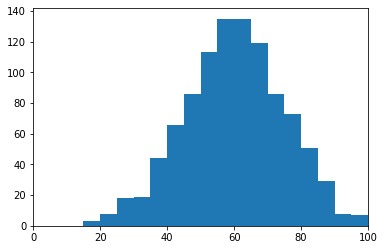
課題7

6.9.8. 課題8

データファイル vector.dat に格納されている2つのベクトルを読み込み，それらの内積を求める関数 dot_file()

def dot_file(filename):
    "filenameから2つのベクトルを読み込み，それらの内積を返す"
    pass

を作成しよう．関数 np.dot() を用いること．ただし，以下のようにvector.datの最初の行にはベクトルの長さ，次の行は空白，ベクトル1の各要素，空白行，ベクトル2の各要素，のようにデータが格納されている．

20                      # データ数
                        # 空白行
1.000000000000000e+00
9.510565162951535e-01
(中略)
8.090169943749473e-01
9.510565162951535e-01
                        # 空白行
0.000000000000000e+00
3.090169943749474e-01
(中略)
-5.877852522924734e-01
-3.090169943749476e-01

np.loadtxt() のオプション skiprows を用いて最初の2行を無視して読み込むと以降のデータが全て1次元配列として返される(区切りの空白行は無視される)ので，この前半と後半をそれぞれ別のベクトルとして処理すればよい．

6.9.9. 課題9

任意の長さの1次元整数型配列に与えられた整数が含まれているかどうかを調べ，含まれていた時には真 ( True ，そうでなければ偽 False )を返す関数 find_var を作成しよう．また同様に，値が含まれていた時にはその要素のインデックスを返し，そうでなければ-1を返す関数 find_var_index() を作成しよう．実装は色々考えられるが， np.any() や np.nonzero() または np.where() などを使うとよい．

これらの関数を

def find_var(x, var):
    "varが配列xに含まれているかどうかを調べる"
    pass

def find_var_index(x, var):
    "varが配列xに含まれている時にはそのインデックスを，そうでない場合は-1を返す"
    pass

のように定義し，以下のように動作を確かめよう．

>>> x = np.random.randint(0, 100, 10)
>>> x
array([17, 75, 28, 83, 93, 20, 19, 94, 62, 61])
>>> find_var(x, 28)
True
>>> find_var(x, 25)
False
>>> find_var_index(x, 28)
2
>>> find_var_index(x, 25)
-1

さらに， np.random.randint() を用いて適当な長さの1次元整数配列を作成し，値を探索してみよう．

6.9.10. 課題10

参考

1次元のセル・オートマトンについては Wikipedia を参照．

1次元のセル・オートマトンを実装しよう．具体的には，以下のような関数を作成し，10進数で与えられたルール decrule に基づいて，一次元配列 x を初期値とし， step 数だけ状態遷移を求めよう．関数の返値は2次元配列で，各ステップ，各セルの状態を表すものとする．ただし，境界の値は初期値のまま固定でよい．

def cellular_automaton(x, step, decrule):
    "初期値xからstep数だけセル・オートマトンによる状態遷移を求める"
    pass

例えば以下の例ではルール90を採用し，初期値として中央のセルのみを1とし，それ以外は0を与えている．

>>> n = 256
>>> m = n//2
>>> xzero = np.zeros((n,), dtype=np.int32)
>>> xzero[m] = 1
>>>
>>> y = cellular_automaton(xzero, m, 90)
>>> plt.imshow(y, origin='lower', cmap=plt.cm.gray_r)

これはシェルピンスキーのギャスケット（下図）を生成することが知られている．

課題10

6.9.11. 課題11

参考

アルゴリズムについては こちら を参照．

逆関数法を使って指数分布

\[P(x) = \lambda \exp ( - \lambda x )\]

に従う乱数を返す関数 randexp()

def randexp(l, n):
    "指数分布に従う乱数をn個作成する"
    pass

を作成しよう．(ただし，実用上は指数分布に従う乱数は numpy.random.exponential() によって得られるので，これを用いればよい．）

この関数を用いて発生させた乱数と解析的な確率分布を以下のように比較しよう．

>>> l = 1.0
>>> r = randexp(l, 60000)
>>> # ヒストグラム
>>> hist, bins = np.histogram(r, bins=np.linspace(0, 12, 33), density=True)
>>> plt.step(bins[0:-1], hist, where='post')
>>> # 解析的な分布
>>> x = 0.5*(bins[+1:] + bins[:-1])
>>> y = l * np.exp(-l*x)
>>> plt.plot(x, y, 'k--')
>>> plt.semilogy()

この結果は以下のようになる．

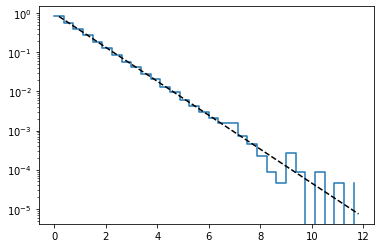
課題11

6.9.12. 課題12

参考

アルゴリズムについては こちら を参照．

モンテカルロ法を用いてN次元超球の体積を求める関数 mc_hypersphere()

def mc_hypersphere(n, nrand):
    "n次元超球の体積をモンテカルロ法で求める"
    pass

を作成しよう．ここで nrand は各次元について発生させる乱数の個数である．

この関数を使って近似値と解析的な値を以下のように比較しよう．

>>> n = 3
>>> nrand = 100000
>>> print('{:20} : {:<20.14e}'.format('Monte-Carlo', mc_hypersphere(n, nrand)))
>>> print('{:20} : {:<20.14e}'.format('Exact', hypersphere(n)))
Monte-Carlo          : 4.18304000000000e+00
Exact                : 4.18879020478639e+00

ただし，解析的な値を返す関数 hypersphere() を別途定義するものとする．

---

[1]

これはPythonに組み込みのライブラリではないので別途インストールする必要があるが，ほとんどの環境には入っていると思われるのでここではあるものとして考える．

[2]

正確にはクラス np.ndarray のインスタンスと呼ぶべきかもしれないが，ここでは細かいことは置いておこう．

[3]

このようにNumPyの数学関数はスカラーに対してもNumPy配列に対しても有効である．さらに，標準の math モジュールよりも多くの数学関数が用意されているので，特に理由がない限りは常にNumPyの数学関数を用いるのが簡単であろう．

[4]

Pythonにも配列を提供する array という組み込みのモジュールがあるのだが，NumPy配列があまりにも便利で普及しているのでそれほどお目にかかることはないだろう．

[5]

NumPyで提供されていないような特殊関数であっても，ほとんどはSciPyの特殊関数モジュール scipy.special に実装されているであろう．ここで提供されていない関数が必要になることは稀である．

[6]

... は Ellipsis Pythonのオブジェクトというものであり，何かが省略されていることを意味する．

[7]

疑り深い人はもっと直接的に確かめてみよう． shares_memory() 関数は与えられた2つのNumPy配列が同じメモリ領域を指しているかどうかをチェックする．これを使うと

>>> np.shares_memory(x, y)
True

のように，確かに x と y が同じメモリ領域を指していることがわかる．

[8]

ただし，unformatted形式は標準化されておらず，コンパイラやエンディアン(CPUの種類)などに依存する形式なので，可能な限りその使用を避けた方が無難である．(比較的新しいストリーム入出力を使えばよい．)