8. 数値解析の基礎
これまでは主にプログラミングの作法を学んできた.基本的には現在までの知識を組み合わせれば原理的にはどんな問題にも対応できるようになっている [1].そこで,これまでに学んだ知識を用いてもう少し実践的な内容に取り組もう.具体的には非線形方程式の求根法や,関数の数値積分,また乱数の使い方などを扱う.
参考
sample1.f90 : 桁落ちと情報落ち
sample2.f90 : 二分法
sample3.f90 : Newton法
sample4.f90 : 数値積分
sample5.f90 : 乱数
8.1. 実数の精度と誤差
これまで何気なく用いてきた実数型だが,数値解析を始める前に計算機における実数の取り扱いやその誤差について理解しておこう.
8.1.1. 浮動小数点数の表現
実数は計算機の内部では浮動小数点数と呼ばれる形式になっており,
のような表現で表される.仮数部は有効桁を決める部分であり,指数部は絶対値を調整するためのものである. 仮数部が \(1.f\) となっているのは(最上位ビットは常に1なので)実質1ビット分だけ精度を稼ぐためである(これをケチ表現と呼ぶ). 例えば標準的な規格(IEEE754規格)では単精度の場合,符号部に1ビット,仮数部に23ビット,指数部に8ビットが割り当てられている. 指数部が8ビットであることから,\(e=0, 1, \ldots, 255\) であり,即ち絶対値の範囲としては \(2^{-127} \sim 10^{-38} \lesssim x \lesssim 2^{127} \sim 10^{+38}\) 程度以内の数値しか表現できない. また \(\log_{10} (2^{23 + 1}) \sim 7.2\) なので10進での有効桁数は7桁程度である. 同様に倍精度では符号部に1ビット,仮数部に52ビット,指数部に11ビットが割り当てられていることから絶対値の範囲は \(2^{-1024} \sim 10^{-308} \lesssim x \lesssim 2^{+1024} \sim 10^{+308}\),有効桁数は \(\log_{10} (2^{52+1}) \sim 15.9\) となり10進での有効桁数は16桁程度である.
8.1.2. 丸め誤差
実数を有効桁で「丸め」て表現することから生じる誤差を丸め誤差と呼ぶ.これは場合によっては求めたい計算結果の精度に悪影響を及ぼすこともあるため,注意が必要である.
桁落ち
絶対値の非常に近い2つの数の差を計算すると絶対値が非常に小さくなり,その分だけ相対誤差が大きくなってしまう.これを桁落ちと呼ぶ.
例えば \(\sqrt{1 + x} - 1\) のような演算は \(x\) が非常に小さい場合にはその誤差が無視できない.簡単のため10進数で有効桁数が5桁の場合を考えよう. \(x=0.001\) とすると, この精度の範囲では \(\sqrt{1 + x} \approx 1.0005\) なので, \(\sqrt{1 + x} - 1 \approx 0.0005\) となり有効桁数が1桁に低下してしまう.これは例えば以下のような式変形によって減算を無くすことで回避が可能である.
情報落ち
絶対値の大きい数に小さい数を加えてもほとんど変化が無い.これを情報落ちと呼ぶ.
同様に有効桁数が5桁の場合を考えよう.\(a = 1.0000\), \(b = 1.0000 \times 10^{-5}\) はどちらとも5桁の有効桁数を持つが, \(a + b = 1.00001\) の小数点第5位は精度は有効桁数の範囲外となるため,情報が失われてしまう.例えば,総和計算の際に非常に大きな数と小さな数を多数加える場合にはこれが問題となることがある.このときには小さい方から順に和を計算することで回避できる.
これらを具体的に示した サンプルコード参照 の実行結果は
1$ ./a.out
2 Cancellation of significant digits
3correct result : 0.500000000000000E-15
4incorrect result : 0.444089209850063E-15
5 Loss of trailing digits
6correct result : 0.100000001000000E+01
7incorrect result : 0.100000001110223E+01
のようになる.3行目と4行目が桁落ち対策ありとなしの比較,6行目と7行目が情報落ちの対策ありとなしの比較である.このように,数学的に等価な演算であっても無視できないような誤差が発生する可能性があることは認識しておくべきである.なお,丸め誤差の影響を調べるのに一番安直だが確実な方法は単精度から倍精度,倍精度から4倍精度に精度を上げてみて結果が変わらないことを確認することである.
8.2. 求根法
解析的には解けない方程式(非線形方程式)の解を求める方法を考えよう.通常は右辺と左辺の両方に式があるわけだが,移項してしまって
という一般的な形にして解くことにしよう.実はこの問題は意外と難しい問題であり,どんな問題にも使うことのできる汎用的で,かつ高速に解を求められるような手法は存在しない.と言うのはどんな手法であっても基本的には初期値として近似解のあたりを付けて,少しずつ真の解に近づけていく反復法だからである.初期値の選び方によっては正しい解に収束しない場合や,欲しい解(例えば物理的な解)に収束しないもあり得る [2].計算機は初期値までは面倒を見てくれないので,人間が適切な初期値を与えてあげなければならない.とりあえず初期値は与えられたとして,そこから近似解を反復によって求めるアルゴリズムを見ていこう.
8.2.1. 二分法
もしある区間に解が1つあると分かっているならば,反復によって近似解が必ず真の解に収束する,二分法(bisection method)と呼ばれるアルゴリズムが知られいる.まず \([x_1, x_2] \ (x_1 < x_2)\) に対して \(f(x_1) < 0, f(x_2) > 0\) ならばこのの区間に解があることが分かる.このとき,二分法によって近似解を求める手順は以下のようなものとなる.
\(x = (x_1 + x_2)/2\) を近似解とする.
\(f(x) < 0\) なら \(x_1 = x\), \(f(x) > 0\) なら \(x_2 = x\) とし,(1)に戻る.
この手順を解が収束するまで繰り返せばよい.収束判定は例えば許容誤差を \(\epsilon\) として \(|x_2 - x_1| < \epsilon\) (区間の幅が許容誤差よりも小さい)などとすればよい.
実際には \(f(x_1) > 0, f(x_2) < 0\) の場合も考慮しなければならないが,組み込み関数 sign を用いてこれは簡単に実現出来る.以下のコードには二分法の実装例を示している.ただし f は関数として定義されているものとする.
27 sig = sign(1.0_8, f(x2) - f(x1))
28 status = .false.
29 do n = 1, nmax
30 x = (x1 + x2) * 0.5_8
31 y = f(x)
32
33 ! 収束判定
34 if(abs(x2 - x1) < tolerance) then
35 status = .true.
36 write(*, fmt='("Converged at step ", i4)') n
37 exit
38 else
39 write(*, fmt='("Error at step ", i4, " = ", e20.8)') n, abs(y)
40 endif
41
42 ! 次の値を推定
43 if(y * sig < 0.0) then
44 x1 = x
45 else
46 x2 = x
47 endif
48 enddo
8.2.2. Newton法
二分法は解の含まれる範囲を正しく指定すれば必ず収束するという利点はあるものの,あまり収束の速いアルゴリズムではなかった.一方で,初期値によっては収束しないかもしれないが,収束するならばその収束自体は速いというアルゴリズムも考えられる.それがここで紹介するNewton法と呼ばれるものである.これは \(f(x)\) に加えてその微分 \(f'(x)\) も用いるのが特徴である.すなわち,近似解 \(x\) が与えられたときに \(x\) の周りでのテイラー展開した
を用いて, \(f(x + \delta) = 0\) とすると
を得る.即ち \(x - f(x)/f'(x)\) を新しい近似解として採用すればよい.大きな特徴は関数の値だけではなく,その微分値(接線)も用いて収束を加速している点である.しかし,当然ながら初期値によっては収束しないことも十分に考えられる(どういった場合であろうか?).以下のコードはNewton法のアルゴリズムを実装したものである.プログラムの構造は二分法の場合とほぼ同様であるが,微分値を返す関数 df も用いている.
14 status = .false.
15 do n = 1, nmax
16 ! 次の値の推定
17 y = f(x)
18 dy = df(x)
19 dx = -y / dy
20 x = x + dx
21
22 ! 収束判定
23 if(abs(dx) < tolerance) then
24 status = .true.
25 write(*, fmt='("Converged at step ", i4)') n
26 exit
27 else
28 write(*, fmt='("Error at step ", i4, " = ", e20.8)') n, abs(y)
29 endif
30 enddo
8.3. 数値積分
次に関数の積分
の数値的な評価を考えよう.区分求積法の原理を思い出せば,積分領域 \([a, b]\) を小さな領域 \(h = (b-a)/N\) に分割し,積分を微小区間の積分の総和で近似すればよいことが分かるだろう.ここで分割数 \(N\) を十分大きくとることができれば,近似式の誤差は十分小さく抑えることができる.\(x_j = a + j h\) とし,微小区間の端点 \([x_{i}, x_{i+1}]\) で与えられた関数値 \(f_{i}, f_{i+1}\) から,関数系を
のように線形近似することで,以下の 台形公式 が得られる.
ここで \(O(h^2)\) は誤差が刻み幅 \(h\) の2乗で小さくなることを意味する.ただし例外として,元の関数系が線形であれば,当然この評価は厳密な積分値を与える.
この考え方をさらに発展させ, \(x_{i-1}, x_{i}, x_{i+1}\) の3点の関数値 \(f_{i-1}, f_{i}, f_{i+1}\) から関数系を2次関数で近似すれば,以下の Simpsonの公式 が得られる.
ここでSimpsonの公式の誤差は \(h\) の4乗に比例する.当然ながら同じ精度を実現するために必要な計算量はSimpsonの公式の方が台形公式よりも小さくて済む.
Fortranプログラム中では \(f(x)\) を関数として定義し,分割数 \(N\) を適当に定めれば do ループによって総和計算をすることで積分値は簡単に求まる.例えば台形公式であれば
22 !
23 ! 台形公式による数値積分
24 !
25 integral = 0.5_8 * (f(x1) + f(x2))
26 do n = 1, nmax - 1
27 integral = integral + f(x1 + dx * real(n, 8))
28 enddo
29 integral = integral * dx
Simpsonの公式を使った場合であれば
34 !
35 ! Simpsonの公式による数値積分
36 !
37 integral = f(x1) + f(x2)
38 ! odd
39 do n = 1, nmax - 1, 2
40 integral = integral + 4.0_8 * f(x1 + dx * real(n, 8))
41 enddo
42 ! even
43 do n = 2, nmax - 2, 2
44 integral = integral + 2.0_8 * f(x1 + dx * real(n, 8))
45 enddo
46 integral = integral * dx / 3.0_8
のように実装することが出来る.ここで f(x) は被積分関数である.
8.4. 乱数
確率的な現象を計算機を用いて模擬する際には乱数を用いることになる.ただし計算機で用いることのできる乱数は擬似乱数と呼ばれ,乱数のように見えるが実際には決定論的な手法に基づき生成される数列である.従って質の良い(周期の長い)乱数を用いなければ,用途によっては乱数とみなすことのできない場合もあるため注意が必要である.
Fortranには乱数を発生させる組込みのサブルーチン random_number が存在する.
1call random_number(x)
とすれば x に区間 \([0,1)\) の一様乱数が代入される.x は実数型(単精度もしくは倍精度)であれば配列でも良い.配列の場合は全ての要素に一様乱数が代入される.
擬似乱数は決定論的な数列であることは既に述べた通りであるが,その初期値を指定することも出来る.これは乱数のシード(seed)と呼ばれ,組込みのサブルーチン random_seed を用いて行うことが出来る.使い方は
シードを格納領域のサイズを取得(サイズはコンパイラ依存)
必要な領域を確保(
allocateを用いる)シードを指定
といった流れとなる.以下のサブルーチン random_seed_clock は計算機の時刻 [3] に応じてシードを指定するものであり,これを用いれば実行する度に(時刻が異なるので)得られる乱数値が異なることが保証される.逆に固定のシードを用いるようにしておくと毎回同じ結果が得られるため,乱数を用いるプログラムをデバッグする際には都合が良い.
75 !
76 ! 乱数のseedをシステムクロックに応じて変更
77 !
78 subroutine random_seed_clock()
79 implicit none
80 integer :: nseed, clock
81 integer, allocatable :: seed(:)
82
83 ! システムクロックを取得
84 call system_clock(clock)
85
86 call random_seed(size=nseed)
87 allocate(seed(nseed))
88
89 seed = clock
90 call random_seed(put=seed)
91
92 deallocate(seed)
93 endsubroutine random_seed_clock
なお, random_seed_clock を使った乱数シードの初期化は sample5.f90 の例のようにプログラムの実行の最初に一度だけ行えば十分である.
8.5. 第8章 演習課題
8.5.1. 課題1
サンプルプログラムをコンパイル・実行して動作を確認せよ.さらに,適宜修正してその実行結果を確認せよ.
8.5.2. 課題2
2次方程式 \(a x^2 + b x + c = 0\) の解は以下の解の公式を用いて求めることが出来る.
しかしこの公式を単純に用いた場合には \(b^2 \gg 4 a c\) の時には,桁落ちによってどちらか一方の解の精度が悪くなってしまう.このことを実際に確認し,式変形によってその精度を改善せよ.
例えば \(a = 1, b = -10^{9}, c = 1\) とした時の解は
であるが,解の公式を用いた場合と式変形によって桁落ち対策をした場合で数値解を比較せよ.(桁落ち対策が必要なのはどちらか一方の解のみである.)
8.5.3. 課題3
Newton法では関数の微分値を解析的に与えて用いるが,割線法(Secant method)と呼ばれる手法では連続した2つの近似解を用いて,微分を差分で近似する.即ち \(n\) 番目の近似解を \(x_n\) と書いたときに,Newton法の公式
において,微分値を以下のように近似する.
(この手法では微分値の計算をする必要がないため,反復1回あたりの計算量が少なくなる可能性があるが,収束はNewton法よりも少し遅くなる.)
この割線法を実装し,以下の方程式
を数値的に解くことで,その収束の速さを二分法およびNewton法と比較せよ.ただし \(M= 1836\) とする.なお解は \(x \simeq -2.5\) なので二分法ではこの前後に2つの初期値を指定すればよい.割線法も2つ初期値が必要になるが,(この関数に関しては)初期値には敏感ではないので,例えば0と1を初期値として用いればよい.ここでは収束の速さを比較すればよいので,各反復ごとの収束判定はせずに20回程度の反復を行い誤差の減少の様子をgnuplotを用いて図示せよ.ただし連続する2つの近似解の差を誤差と定義する.
結果は以下の例ようになるであろう.
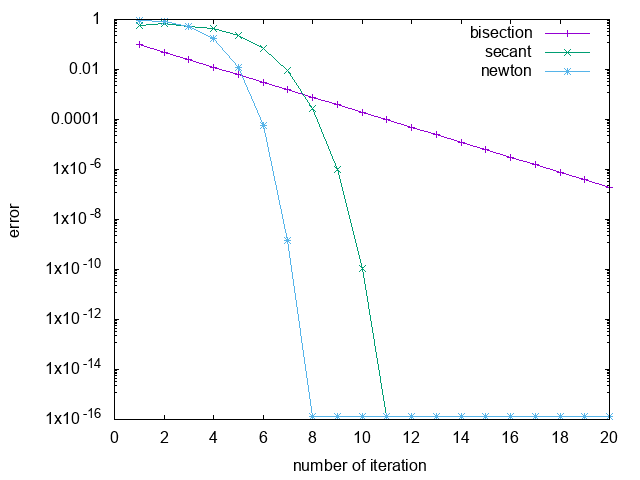
求根法の収束比較
8.5.4. 課題4
\(f(x) = \dfrac{4}{\pi} \dfrac{1}{1 + x^2}\) および \(f(x) = (n+1) \ x^{n} \ (n = 0, \ldots, 5)\) のそれぞれについて
の積分を台形公式およびSimpsonの公式で数値的に行い,誤差の分割数に対する依存性をgnuplotを用いて図示せよ.例えば分割数を \(2^{n} (n=1, 2, \ldots, 16)\) の範囲で変えて依存性を調べれば良い.
例として \(f(x) = \dfrac{4}{\pi} \dfrac{1}{1 + x^2}\) について誤差をプロットすると以下のようになるであろう.
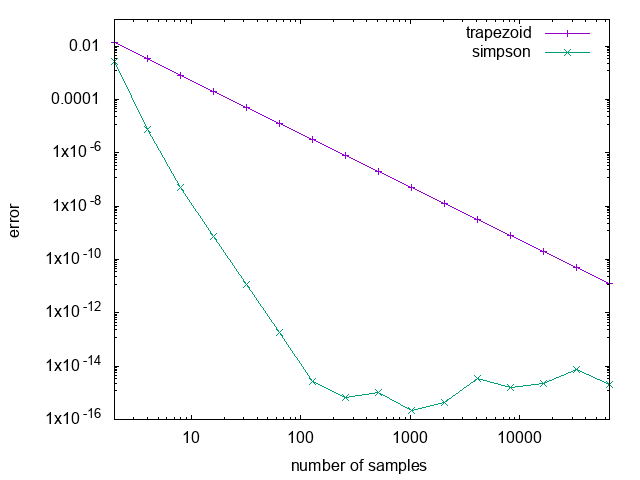
数値積分誤差の分割数依存性
このような依存性となる理由を考えよう.
8.5.5. 課題5
一様乱数を用いてある確率分布に従う乱数を発生させるために逆関数を用いる方法(変換法や逆関数法などと呼ばれる)を考える.区間 \([0, 1)\) での一様乱数 \(x\) およびその確率分布 \(f(x)\) ,また必要な乱数 \(y\) とその確率分布 \(g(y)\) とする.ただし乱数の値域は \(a \leq y < b\) とする. \(y\) を \(x\) から何らかの変換で \(y = P(x)\) のように表すとき,確率密度の保存から
が成り立つ.(最後の等式は一様乱数であることから自明である.) この両辺を積分して
によって関数 \(G(y)\) を定義する.ただし \(G(a) = 0\) , \(G(b) = 1\) となるように規格化した.これより
を得る.即ち, \(G^{-1} (x)\) を解析的に求めることができれば,一様乱数 \(x\) を用いて必要な確率分布 \(g(y)\) に従う乱数を作ることができる.(以下の図を参照)
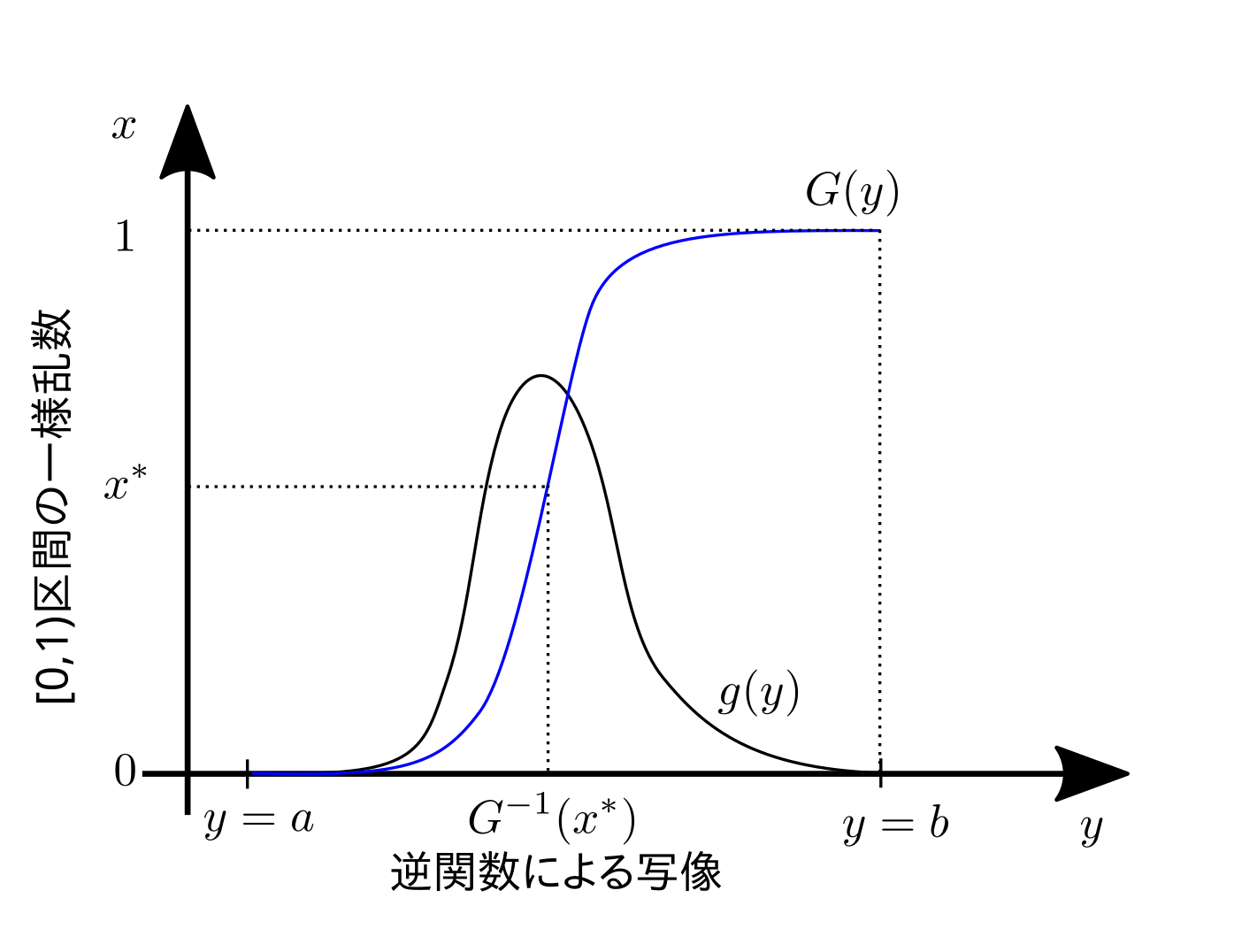
逆関数法の概念図
このことを用いて指数分布
に従う乱数分布を発生させるプログラムを作成せよ.また分布のヒストグラムを作成し,gnuplotを用いてヒストグラムを解析的な分布と共に図示し,乱数の発生数を増やした時に乱数分布が真の分布に近づくことを確かめよ.
以下は60000個の乱数を発生させた場合のヒストグラムの例である.
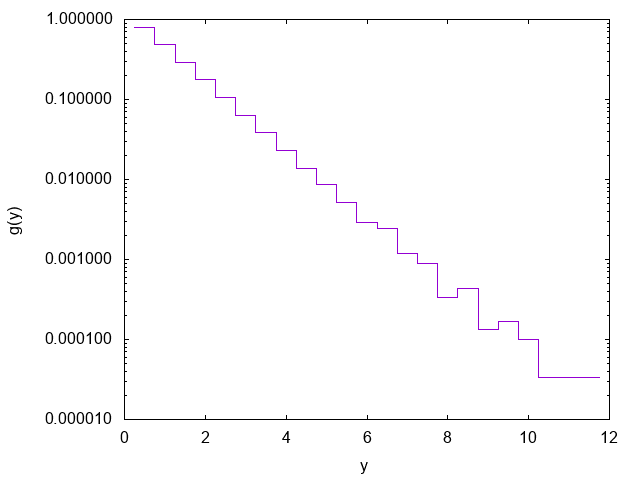
指数分布のヒストグラム
8.5.6. 課題6 †
乱数を利用した数値積分法としてモンテカルロ法が知られている.これを用いて \(n\) 次元ユークリッド空間における単位超球の体積 \(V_n\) を求めるプログラムを作成せよ.
ただし \(n\) 次元超球の体積は \(n\) 次元空間の座標を \(x_i \, (i=1, \ldots, n)\) とし,
なる領域の体積と定義される.ここで対称性から \(0 \leq x_i \leq 1\) の領域のみを考えれば,この体積は \(V_n / 2^{n}\) となる.従って \(n\) 個の一様乱数 \(0 \leq x_i < 1 \, (i=1, \ldots, n)\) を発生させ,上式の条件を満足するかどうかを調べる試行を多数回行い,その確率を求めることによって \(V_n / 2^{n}\) を推定すればよい.
なお真の値は
によって与えられる.
例えば次元数と試行回数を標準入力から与える形式のプログラムの実行結果は以下のようになる.この例のように誤差は試行回数 \(m\) に対して, \(1/\sqrt{m}\) に比例して減少する.
1$ ./a.out
22 1000 # キーボード入力(2次元,試行回数1000回)
3approximation = 0.32240000E+01
4exact value = 0.31415927E+01
5relative error = 0.26231044E-01
6$ ./a.out
72 100000 # キーボード入力(2次元,試行回数100000回)
8approximation = 0.31430400E+01
9exact value = 0.31415927E+01
10relative error = 0.46067683E-03