4. 制御構造

ここではプログラムの動作を制御するための文法について学ぼう．と言っても覚えなければいけないことは if による条件分岐，do による繰り返し，select による条件分岐のみである．goto という構文も存在するのだが，これはバグのもとになることから一般的には使わないほうが良いとされており，従ってここでも敢えて扱わない．

参考

4.1. 条件分岐(if)

if による条件分岐は例えばユーザーの入力によって動作を変更する場合などに用いる．典型的な使い方は以下のようなものである．（これは閏年の判定例である．）

sample1.f90 抜粋
 4  integer :: year
 5
 6  ! 標準入力から整数を読み込む
 7  write(*, *) 'Input year: '
 8  read(*, *) year
 9
10  ! 基本的なifによる分岐
11  if(mod(year, 400) == 0) then
12    write(*, *) 'Leap year'
13  else if(mod(year, 100) == 0) then
14    write(*, *) 'Common year'
15  else if(mod(year, 4) == 0) then
16    write(*, *) 'Leap year'
17  else
18    write(*, *) 'Common year'
19  endif

このように if に続く () の中に条件式(conditional)を記述し，その条件が真( .true.)の時には then に続く処理が実行され，偽( .false.)の時には else if または else で更に条件判定をすることになる．また

1if( conditional ) then
2  ! 処理
3end if

や

1if( conditional ) then
2  ! 処理1
3else
4  ! 処理2
5end if

のように書くことも出来る．構文自体はそれほど難しくないので，ここで注意すべきは条件判定の部分だけであろう．以下の表に条件式に用いられることの多い演算子をまとめてある．なおFortran 77では > のような演算子(関係演算子と呼ばれる)は正式にはサポートされていなかった．このため古いコードには .gt. のような演算子を見かけることもあるかも知れないが，自分で新しくプログラムを作成する際にはこのような古い形式は使うべきではない．新しい形式は /= 以外のものについてはC言語を始めとする他の多くの言語と同じなのでこちらを用いることを強く推奨する．ちなみにC言語などでは /= ではなく != が用いられる．

特に実数の値が等しいかどうかを判定する際には注意が必要である．すなわち，実数に対しては == を使うことは出来ない．なぜなら2つの実数がほぼ等しいように見えても == による判定では全てのビットが厳密に等しくなければ真とは判定されないからである．従って，代わりに例えば差の絶対値 abs(A-B) が十分小さいかどうかで判定しなくてはならない [1]．

条件演算子

演算子

Fortran 77形式

意味

A >  B

A .gt. B

A の方が B よりも大きければ真

A >= B

A .ge. B

A が B 以上であれば真

A <  B

A .lt. B

A の方が B よりも小さければ真

A <= B

A .le. B

A が B 以下であれば真

A == B

A .eq. B

A と B が厳密に等しければ真

A /= B

A .ne. B

A と B が等しくなければ真

また条件判定が複雑な時には以下の論理演算子を用いることになるだろう．

論理演算子

演算子

意味

使い方

.and.

論理積

(条件式1) .and. (条件式2)

.or.

論理和

(条件式1) .or.  (条件式2)

.not.

否定

.not. (条件式)

.eqv.

論理等価

(条件式1) .eqv. (条件式2)

.neqv.

論理非等価

(条件式1) .neqv. (条件式2)

使い方は例えば

1integer :: n
2
3if ( 2 < n .and. n < 5 ) then
4  write(*,*) 'n is larger than 2 and smaller than 5'
5end if

と言った具合である．2 < n < 5 のような数学的な書き方はできないので注意が必要である．

さらに複雑な条件分岐の場合には以下のように if 文を入れ子で使うことも出来る．

1if ( conditional 1 ) then
2  if ( conditional 2 ) then
3    ! 処理1
4  else
5    ! 処理2
6  end if
7end if

ただし何重にも深く入れ子になった if 文の実行効率はあまり良くないので出来るかぎり浅い条件分岐に留めておいた方が良い．

以下は sample1.f90 の11-19行目の閏年の判定と全く同じことを入れ子にした if で実装した例である．

sample1.f90 抜粋
21  ! 同じことを入れ子のifで実現
22  if(mod(year, 4) == 0) then
23    if(mod(year, 100) == 0) then
24      if(mod(year, 400) == 0) then
25        write(*, *) 'Leap year'
26      else
27        write(*, *) 'Common year'
28      endif
29    else
30      write(*, *) 'Leap year'
31    endif
32  else
33    write(*, *) 'Common year'
34  endif

4.2. 反復処理(do)

4.2.1. 決まった回数の繰り返し(do)

決まった繰り返しの処理をするために用いるのが do (従ってこの反復処理は do ループと呼ばれる)である．これも使い方は至ってシンプルである．

sample2.f90 抜粋
10  write(*, *) '--- Do loop #1 ---'
11  sum = 0
12  do i = 1, 10
13    sum = sum + i
14    write(*, *) i, sum
15  enddo

は1から10までの和を順次求めながら結果を出力している．より一般には

1do i = lower, upper, stride
2  ! 繰り返し処理
3end do

のような形で書くことになる．上の例では整数型変数 i は do 変数と呼ばれ，do ループの中で i の値が lower から upper まで stride ずつ変化する．stride は省略することも可能であり，その場合は 1 と解釈される．また stride は負の値であっても良い(当然この時は lower > upper でなければループ内の処理は実行されない)．通常 do 変数は整数型でなければならないが，実数型などでもコンパイル出来てしまう環境もあり，そのような場合は思わぬバグの原因となってしまう．間違いを未然に防ぐためにも do 変数には整数型を用いること．

例えば次は先ほどの例の和を求める処理を1つおきに実行する．

sample2.f90 抜粋
18  write(*, *) '--- Do loop #2 ---'
19  sum = 0
20  do i = 1, 10, 2
21    sum = sum + i
22    write(*, *) i, sum
23  enddo

また if 文の場合と同様に do ループに関しても以下のように入れ子(多重ループ)にすることが出来る．以下は2重ループの例である．

sample2.f90 抜粋
34  write(*, *) '--- Do loop #4 ---'
35  do i = 1, 3
36    do j = 1, 3
37      write(*, *) '(', i, ',', j, ') => ', 3 * (i - 1) + j
38    enddo
39  enddo

この部分の実行結果は以下のようになる．

 1--- Do loop #4 ---
 2 (           1 ,           1 ) =>            1
 3 (           1 ,           2 ) =>            2
 4 (           1 ,           3 ) =>            3
 5 (           2 ,           1 ) =>            4
 6 (           2 ,           2 ) =>            5
 7 (           2 ,           3 ) =>            6
 8 (           3 ,           1 ) =>            7
 9 (           3 ,           2 ) =>            8
10 (           3 ,           3 ) =>            9

4.2.2. 条件を指定した繰り返し(do while)

繰り返しの処理には基本的に先ほどの do ループを用いれば良いのだが，これを少し違った形式で行う do while なる構文も用意されている．これは

1do while( conditional )
2  ! 繰り返し処理
3end do

のような形で用い，() 内の条件式が真( .true.)の間は繰り返し処理が行われる．例えば

 1integer :: i
 2real(8) :: sum
 3
 4i = 1
 5sum = 0
 6do while(i <= 10)
 7   sum = sum + i
 8   i = i + 1
 9   write(*,*) i, sum
10end do

は先ほどの例 sample2.f90 の最初の do ループと同じ処理を実行する．この場合はあえて do while を用いる意味はあまり感じられないが，繰り返し回数が予め分からない処理ではこのような形式を用いるとスマートに書ける場面にもしばしば遭遇する．例えば反復計算によって実数型の値の収束判定をする場合などは

1real(8) :: x
2
3do while(abs(x) > 1.0e-8_8)
4  ! 繰り返し処理
5end do

などのように非常にスッキリと記述できる．この例では abs(x) の値が \(10^{-8}\) 以下になるまで反復を続ける．例えば，以下は逐次計算によって平方根を求める計算である．

sample3.f90 抜粋
20  !
21  ! 逐次近似によって平方根を求める
22  !
23  do while(abs((sqrt_x0 - sqrt_x1) / sqrt_x0) > tolerance)
24    sqrt_x0 = (sqrt_x0 + sqrt_x1) * 0.5_8
25    sqrt_x1 = x / sqrt_x0
26  enddo

4.2.3. 複雑な処理(exitとcycle)

単純な繰り返しだけでなく，より柔軟な制御を行うには exit や cycle を用いる．exit では do ループの中から途中で抜けることが出来，cycle ではループ内のそれ以降の処理を行わずにループ先頭に戻ることがで出来る．これらを用いると意図的に作った無限ループから条件を満たした時だけ抜け出すようなプログラムも簡単に作ることができる．例えば以下の例を見てみよう．

sample4.f90 抜粋
 9  ! 無限ループ
10  do while(.true.)
11    ! 標準入力から読み込む
12    write(*, *) ''
13    write(*, *) 'Input a positive integer (less than 10): '
14    read(*, *) increment
15
16    if(increment <= 0) then
17      write(*, *) 'error : input <= 0'
18      exit   ! ループを抜ける
19    else if(increment >= 10) then
20      write(*, *) 'error : input >= 10'
21      cycle  ! ループの先頭へ(これ以下の処理は行わない)
22    endif
23
24    ! countを増やす
25    count = count + increment
26
27    write(*, *) 'current count = ', count
28  enddo

この例では標準入力からの10より小さい正の整数を受け取り，受け取った数の和を求める．ただし0以下の値を受け取った場合は処理を終了する．また，10以上の値受け取った場合はエラーを表示し，和はとらずに無視する．実行結果は例えば以下のようになる．

 1$ ./a.out
 2 Input a positive integer (less than 10):
 35                                            # キーボード入力
 4 current count =            5
 5
 6 Input a positive integer (less than 10):
 74                                            # キーボード入力
 8 current count =            9
 9
10 Input a positive integer (less than 10):
1110                                            # キーボード入力
12 error : input >= 10
13
14 Input a positive integer (less than 10):
150                                            # キーボード入力
16 error : input <= 0
17 last count =            9

なお，同じ動作を実現する方法は1つとは限らない．例えば while の条件判定を increment <= 0 と変更すれば，この条件に対応する if は必要がなくなる．複数の方法がある場合にはより分かりやすい方(すなわち間違いが発生しにくい方)を採用すれば良い．ちなみに無限ループを作るには while (.true.) は必ずしも必要では無く，

1do
2  ! exitで抜けないかぎりここの処理が無限に繰り返される
3end do

のように書くことも可能である．

4.3. 条件分岐(select)

select 構文を用いても条件分岐を行うことも出来る．基本的には if を用いれば同じことは実現出来るのだが，場合によっては select を用いた方がよりスッキリとした形で書ける事があるので知っておいて損はない．典型的には整数や文字列の値で場合分けを制御する際に用いる(実数型には用いることは出来ない)．

一番基本的な使い方は以下のようなものである．

sample5.f90 抜粋
 7  ! 整数を読み込む
 8  write(*, *) 'Input integer : '
 9  read(*, *) i
10
11  ! 整数の値で場合分け
12  select case(i)
13  case(0)        ! i == 0 のとき
14    write(*, *) 'your input was zero'
15  case(1)        ! i == 1 のとき
16    write(*, *) 'your input was one'
17  case(2)        ! i == 2 のとき
18    write(*, *) 'your input was two'
19  case(3)        ! i == 3 のとき
20    write(*, *) 'your input was three'
21  case default   ! 上記以外全て
22    write(*, *) 'your input was too large'
23  endselect

case で入力された整数の値に応じて処理を切り替えている．また，どの case の条件にも当てはまらない場合の処理は case deafault によって行えば良い．

この例を見ただけでは if-elif-else を使うのとほとんど変わらないように感じられるので，もう少し select の利点が生かされた例として以下を見てみよう．ここでは入力された整数 score (テストの点だと思おう)の値によって場合分けをしている．

sample5.f90 抜粋
26  write(*, *) ''
27  write(*, *) 'Input score : '
28  read(*, *) score
29
30  select case(score)
31  case(0)              ! 0点
32    write(*, *) 'zero'
33  case(1:29)           ! 1-29点
34    write(*, *) 'poor'
35  case(30:59)          ! 30-59点
36    write(*, *) 'fair'
37  case(60:89)          ! 60-89点
38    write(*, *) 'good'
39  case(90:100)         ! 90-100点
40    write(*, *) 'excellent'
41  case default         ! それ以外
42    write(*, *) 'invalid input'
43  endselect

この例のように case では単一の値だけでなく値の範囲を指定することができる．範囲の指定は case(下限:上限) のような形ですれば良い．

さらに

sample5.f90 抜粋
47  write(*, *) 'Input language : '
48  read(*, *) c
49
50  ! 文字列の値で場合分け
51  select case(c)
52  case('c', 'c++', 'fortran')
53    write(*, *) 'compiled language'
54  case('python', 'perl', 'ruby')
55    write(*, *) 'script language'
56  case('english', 'japanese', 'french', 'chinese')
57    write(*, *) 'natural language'
58  case default
59    write(*, *) 'others'
60  endselect
61
62  stop

は文字列の値によって分岐する例である．このように1つの case で複数の値をカンマで区切って指定することも出来る．

4.4. 第4章 演習課題

参考

4.4.1. 課題1

サンプルプログラムをコンパイル・実行して動作を確認せよ．さらに，適宜修正してその実行結果を確認せよ．

4.4.2. 課題2

標準入力から2つの整数( \(n, m\) とする)を読み込み，その大小を比較するプログラムを作成せよ．例えば \(n = 1, m = 2\) なら以下のように 1 is smaller than 2 と表示する．

1$./a.out
2 Input two integers:
31    # キーボード入力
42    # キーボード入力
5           1  is smaller than            2

同様に \(n = 2, m = 1\) なら 2 is larger than 1, \(n = m = 1\) なら 1 is equal to 1 などと表示するものとする．

4.4.3. 課題3

\(0^\circ\) から \(180^\circ\) まで \(10^\circ\) 刻みの \(\theta\) および， \(\sin \theta\), \(\cos \theta\) を標準出力に表示するプログラムを作成せよ(以下のように各 \(\theta\) の値ごとに改行せよ)．またこの結果をリダイレクトを用いてファイルとして記録し，gnuplotを用いてこのファイルのデータとgnuplotに組み込みの三角関数を共に図示せよ．なお三角関数の引数はラジアン単位であることに注意せよ．

実行結果は例えば以下のようなものになる．

1$ ./a.out
2   0.0000000000000000        0.0000000000000000        1.0000000000000000
3   10.000000000000000       0.17364817766693033       0.98480775301220802
4   ... 省略 ...
5   170.00000000000000       0.17364817766693069      -0.98480775301220802
6   180.00000000000000        1.2246467991473532E-016  -1.0000000000000000

以下のようにリダイレクトでデータファイルを作成した場合には

1$ ./a.out > data.dat

gnuplotでは

1> plot   'data.dat' using 1:2 w lp, sin(x/180*pi)
2> replot 'data.dat' using 1:3 w lp, cos(x/180*pi)

などとして結果を確認すればよい．

4.4.4. 課題4

標準入力から与えられた2つの整数\(m, n \ge 1\) の最大公約数を表示するプログラムを作成せよ．最大公約数を求めるには以下のアルゴリズム(ユークリッドの互除法)を用いるとよい．

  1. \(m\) を \(n\) で割った余り \(r\) を求める．

  2. もし \(r = 0\) ならば \(n\) が最大公約数である．

  3. もし \(r \neq 0\) ならば， \(m\) に \(n\) を， \(n\) に \(r\) を代入して[1]に戻る(繰り返す)．

実行結果は例えば以下のようなものになる．

1$ ./a.out
212
320
4 Greatest common divisor :            4

なお，組み込み関数 mod を用いて

1r = mod(m, n)

とすれば m を n で割った余りを r に代入することが出来る．

4.4.5. 課題5

以下の級数計算により自然対数の底 \(e\) の近似値を求めるプログラムを作成せよ．

\[e \simeq \sum_{n=0}^{N} \frac{1}{n !}. \quad (0! = 1に注意せよ)\]

ただし以下の条件を満たすこと．

  • 上式の \(N\) および許容誤差 \(\epsilon\) を標準入力から読み込む．

  • \(N > 1\) でない場合および \(0 < \epsilon < 1\) でない場合にはエラーメッセージを表示して終了する．

  • 誤差が \(\epsilon\) 以下になった時点か， \(n = N\) まで計算した時点で級数計算を打ち切る．

  • 最後に収束したかどうか，最終的な項数 \(n\) ，真値，近似値，相対誤差を表示して終了する．

実行結果は例えば以下のようなものになる．

1$ ./a.out
210          # キーボード入力
31.0e-8      # キーボード入力
4 Did not converge !
5 N                  :           10
6 Exact value        :    2.7182818284590451
7 Approximated value :    2.7182818011463845
8 Error              :   1.00477663102110533E-008

4.4.6. 課題6

標準入力から文字列(英単語)を読み込み，それが food, animal, vehicle, others (それ以外)のいずれかを判定し，表示するプログラムを作成せよ．ただし exit が入力されるまでプログラムは終了せず何度でも入力を受け付けるものとする．なお以下の英単語リスト以外のものは others と判断してよい: apple, orange, banana, dog, cat, lion, car, airplane, motorcycle ．

実行結果は例えば以下のようなものになる．

 1$ ./a.out
 2apple    # キーボード入力
 3 food
 4cat      # キーボード入力
 5 animal
 6car      # キーボード入力
 7 vehicle
 8dog      # キーボード入力
 9 animal
10airplane # キーボード入力
11 vehicle
12bike     # キーボード入力
13 others
14exit     # キーボード入力
15 Now exit program...

4.4.7. 課題7

以下の漸化式

\[p_{n+1} = p_n + \alpha p_n (1 - p_n)\]

で定義される数列 \(p_n (n=0, 1, \ldots)\) を考える．初期値 \(p_0 = 0.9\) から数列を生成し，そのうち \(n=100, \ldots, 200\) までを \(\alpha\) の関数として \(1 < \alpha < 3\) の範囲でプロットせよ． \(\alpha\) を \(10^{-3}\) 刻みで変えながらプロットすると結果は以下のようになるだろう．

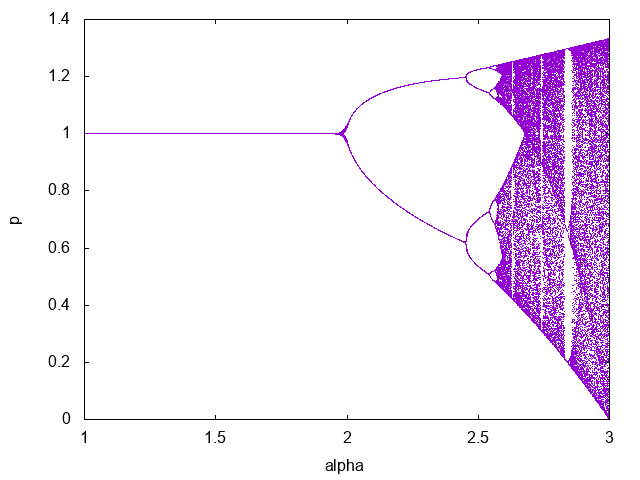
_images/logistic.png

ロジスティック写像

このような写像はロジスティック写像と呼ばれ，非常に単純な式ながら一定の条件を満たすときにはカオスを生み出すことが知られている．