10. 付録

参考

10.1. 大規模なプログラム開発

10.1.1. 分割コンパイル

これまでは基本的に単一のソースファイルからなるプログラムを扱ってきたが，大規模なプログラムを扱う際にはソースファイルをいくつかに分割して扱うと開発の見通しが良くなる．複数のソースファイルからなるプログラムを開発するにあたって，まずは単一のソースファイルから実行形式のファイルを作る手順を復習しよう．

これまでは例えば

1$ gfortran sample.f90

によってソースファイルから実行ファイル a.out を作成してきた．これは実際には コンパイル と リンク という2つのステップを同時に行うものである．

コンパイルとはソースファイルを解釈し，機械語に変換する作業である．機械語に変換されたファイルを オブジェクトファイル と呼び，通常は拡張子 .o が用いられる．オブジェクトファイルを生成するには

1$ gfortran -c sample.f90

のように -c オプションを付けてコンパイルする．この結果，この例では sample.o が生成される．生成されたオブジェクトファイルは機械語になってはいても，実際にプログラムを実行可能な形式にはなっておらず，関数やサブルーチンなどの単位で個別に機械語になっているだけである．実行形式に変換するには，それらの自分で実装したものに加え，組み込み関数( read ，write なども実際には組み込み関数の1種である)などを連結する作業が必要である．組み込み関数などのまとまりを標準ライブラリと呼び，この連結作業をリンクと呼ぶ．

オブジェクトファイルをリンクするには

1$ gfortran sample.o

とすればよい．この例では sample.o と標準ライブラリがリンクされ，実行可能なファイル(この例では a.out )が生成される．

次に複数のファイルからなるプログラムの場合を考えよう．例えばメインプログラムが定義されている sample1.f90 が sample1a.f90 に，また sample1a.f90 が sample1b.f90 に依存している場合には

1$ gfortran sample1b.f90 sample1a.f90 sample1.f90

のようにすれば，コンパイルとリンクを1つのコマンドで同時に実行することができる(順番に注意)．これは実際には以下のように各ファイルを個別にコンパイルし，最後に全体をリンクする作業に相当する．

1$ gfortran -c sample1b.f90
2$ gfortran -c sample1a.f90
3$ gfortran -c sample1.f90
4$ gfortran sample1b.o sample1a.o sample1.o

リンク時には与えられた全てのオブジェクトファイルに加えて，常に標準ライブラリがリンクされる．

このように分割コンパイルを用いる利点は，コンパイル時間の短縮にある．個別にコンパイルが出来るので，ソースファイルを更新した場合には，その必要なファイルだけを再コンパイルすれば良い．なお，リンクにかかる時間は通常短く，コンパイル時間に対しては無視できる．従って，頻繁に修正をしながらテストする場合などでは，実行ファイルの作成にかかる時間を短縮できることになる．

なお，Fortranでモジュールを用いる場合は gfortran -c によるコンパイルで .mod という拡張子のファイル(例えばモジュール名が test なら test.mod )が生成される．別ファイルのモジュールを利用する際には，この .mod ファイルが無いとコンパイル出来ないので注意しよう [1]．また他のディレクトリに .mod ファイルがある場合には，-I オプションを用いてコンパイラが .mod ファイルを探す場所を指定することが出来る [2]．

1$ gfortran -c -I../module sample.f90

のように実行すれば，カレントディレクトリに加えて ../module にある .mod ファイルも参照することになる．規模が大きなプログラムではいくつかのディレクトリにファイルを分散して配置するようになるため，-I オプションを頻繁に用いることになるだろう．

10.1.2. ライブラリの利用方法

一般に，関数やサブルーチン群をひとまとまりにしたものをライブラリと呼ぶ．これまでにも組み込み関数などの標準で用意されている便利な機能を利用してきたが，これは標準ライブラリが提供するものである．これと同じように，他の誰かが開発した便利な関数やサブルーチンを自分のプログラムから呼び出して利用することも出来る．

ライブラリは通常(Unix系のOSでは) libABC.a や libXYZ.so といったファイル名になっている(これらをアーカイブとも呼ぶ)．基本的には実行形式のファイルを作成するリンク時にこれらのライブラリともリンクするように指定してやれば良い．例えば

1$ gfortran main.o -lABC -lXYZ

とすれば libABC.a，libXYZ.so の両方とリンクすることが出来る．このようにライブラリとリンクするには，拡張子とファイル先頭の lib を除いたライブラリ名を -l オプションに渡せば良い．ただし，ライブラリファイルがあるディレクトリがカレントディレクトリや標準の場所(通常 /usr/lib や /usr/local/lib など)以外の場合にはその場所を -L オプションで明示的に指定してやらなければならない．以下の例では libABC.a が ../lib にある場合に，それを明示的に指定してリンクを実行する．

1$ gfortran main.o -L../lib -lABC

10.1.3. GUIプログラムの作成 †

10.1.4. Makeの使い方

To be written.

10.2. 関数やサブルーチンの引数渡し

関数やサブルーチンの引数として，関数やサブルーチンを渡すことが出来る．これには以下のように引数として渡す関数やサブルーチンの形式を interface を用いて指定する．

 1subroutine writefunc(f, x)
 2  implicit none
 3  real(8), intent(in) :: x
 4
 5  ! 引数として受け取る関数の形式
 6  interface
 7     function f(x) result(y)
 8       real(8), intent(in) :: x
 9       real(8) :: y
10     end function f
11  end interface
12
13  write(*,'("f(", e12.5, ") = ",  e12.5)') x, f(x)
14
15end subroutine writefunc

より実用的な例として二分法のアルゴリズムを実装した以下の様なモジュール(抜粋)を考えよう．bisection というサブルーチンは関数 \(f(x)\) を引数として受け取り，\(f(x) = 0\) の解を求める．このようなモジュールを定義しておけば，\(f(x)\) の具体的な形が変わってもメインプログラムで bisection の引数として渡す関数を変更するだけで良い．このように，汎用性の高いモジュールを作成しておくことで再利用が非常に簡単になる．

なお，このサブルーチンでは最大の反復回数や許容誤差は optional 属性の引数となっていることにも着目して欲しい．これらが与えられない場合にはモジュール内で定義されたデフォルトの値を用いるようになっている．

 1module mod_bisection
 2  implicit none
 3  private
 4
 5  integer, parameter :: default_maxit = 50
 6  real(8), parameter :: default_tol   = 1.0e-8_8
 7
 8  public :: bisection
 9
10contains
11  ! 二分法により与えられた方程式の解を求める
12  subroutine bisection(f, x1, x2, error, status, maxit, tol)
13    implicit none
14    real(8), intent(inout) :: x1, x2
15    real(8), intent(out) :: error
16    integer, intent(out) :: status
17    integer, intent(in), optional :: maxit
18    real(8), intent(in), optional :: tol
19    ! 引数として関数を受け取る
20    interface
21       function f(x) result(y)
22         real(8), intent(in) :: x
23         real(8) :: y
24       end function f
25    end interface
26
27    integer :: i, n
28    real(8) :: x, y, sig, tolerance
29
30    ! 最大の反復回数
31    if (.not. present(maxit)) then
32       n = default_maxit
33    else
34       n = maxit
35    end if
36
37    ! 許容誤差
38    if (.not. present(tol)) then
39       tolerance = default_tol
40    else
41       tolerance = tol
42    end if
43
44    !
45    ! 以下略
46    !
47
48  end subroutine bisection
49
50end module mod_bisection

なお bisection.f90 で上記モジュールが定義されており，sample3.f90 がこれを用いるメインプログラムである．これをコンパイルするには

1$ gfortran -c bisection.f90
2$ gfortran -c sample3.f90
3$ gfortran sample3.o bisection.o

もしくは

1$ gfortran bisection.f90 sample3.f90

とすれば良い．

10.3. 計算時間の測定

プログラム全体の実行時間はシェルコマンドで計測できる．例えば time コマンドを用いて以下のように実行すれば良い [3]．realの行が実際の実行時間を示している．大雑把には全実行時間のうち，userが自分のプログラムの処理が動いていた時間，sysはOSの処理が動いていた時間を表す．

1$ /usr/bin/time ./a.out
2       0.98 real         0.97 user         0.00 sys

アルゴリズムによる実効速度の違いを検証したり，プログラムのチューニングをするようになってくると，プログラムのある特定の部分の実行時間を測定する必要が出てくる．ここでは cpu_time という組込みサブルーチンを使った時間計測のサンプルプログラムを以下に示す．

実行結果は以下のようになる．

1$ ./a.out
2CPU Time [sec] :   0.8601E+00

サンプルプログラムでは9-12行目の処理にかかる時間を計測している．cpu_time の呼び出しによって引数に現在の時刻が秒単位で代入されるので，計測したい部分の前後でこの値の差をとればよい．ただし正確に計算時間を計測する際には以下のようにいくつか注意が必要である．

  • write や read のようなI/O(入出力)は避ける.これらは非常に時間のかかる処理であるので，入出力があると純粋な計算時間を正確に測ることが出来ない．

  • 計測対象がある程度時間のかかる処理(例えば \(\gtrsim 1\) 秒)であること．cpu_time の返す時刻の精度は \(1 \mu s\) 程度である．

  • 何度か同じ計測をしてばらつきを見ること．現在のほぼ全ての計算機はマルチタスクOSであり，多くの処理を同時に行なっているため，ユーザーが実行しているプログラムの処理に全てのリソースが使われるわけではない．たまたま他のプログラムが走っているタイミングで実行された場合にはパフォーマンスがでない可能性がある．

なお，細かいことを言うと経過時間(elapsed time)，CPU時間(cpu time)，システムCPU時間(system cpu time)，ユーザーCPU時間(user cpu time)で意味が少しずつ異なることに注意しよう．cpu_time で計測されるのはCPU時間である．

10.4. ポインタとデータ構造 †

ポインタとは簡単に言えば別名である．即ち，ポインタ変数は他の変数や配列によって保持されているデータ領域のメモリ上のアドレス(番地)を指し示す変数になっている．例えば，ポインタ変数に対する処理として記述しておけば，ポインタ変数の指し示すアドレスを変更するだけで異なるデータに対する処理を行っていることになる．

しかし，ポインタはこれまで出てきたような処理には敢えて用いる必要が無いので，あまりありがたみを感じられないかもしれない．実際にはポインタはリストやスタック，キューなどのより複雑な データ構造 を記述するには必須であるが，そうでなければ必ずしも必要にはならない．ポインタは初心者には少し難しいかもしれないので，分からなければとりあえずは無視しても良い．

10.4.1. ポインタ変数

ポインタを用いるには変数宣言に pointer 属性を指定すれば良い．またポインタが指し指すことの出来る変数(ターゲット変数)には target 属性を指定する必要がある．以下の例を考えよう．

 1integer, pointer :: iptr
 2integer, target  :: i, j
 3
 4i = 5
 5j = 9
 6
 7! 出力は iptr = 5, i = 5, j = 9
 8iptr => i
 9write(*,'(" iptr = ", i3, ", i = ", i3, ", j = ", i3)') iptr, i, j
10
11! 出力は iptr = 9, i = 5, j = 9
12iptr => j
13write(*,'(" iptr = ", i3, ", i = ", i3, ", j = ", i3)') iptr, i, j
14
15! 出力は iptr = 0, i = 5, j = 0
16iptr = 0
17write(*,'(" iptr = ", i3, ", i = ", i3, " j, = ", i3)') iptr, i, j

8行目の iptr => i によって iptr は i のアドレスを指すことになる( iptr が i の別名となる)ので，9行目の出力では"iptr = 5, i = 5, j = 9"となる．同様に12行目の iptr => j によって iptr は j のアドレスを指すことになる．また，16行目の iptr = 0 は iptr の指すアドレスへの代入なので，この結果 iptr だけでなく j の値も変更されることになる．この代入文のように，ポインタ変数に対しても通常の変数のように任意の演算が可能である [4]．

なお nullify によってポインタ変数とターゲット変数との結合を解除することが出来る．またポインタは 無名領域 (他の変数によって指し示されていない領域)との結合も可能である．これは動的配列の場合と同様に allocate によって行い，この場合の結合の解除は( nullify では無く) deallocate によって行う．また，結合状態を検査するための組込み関数 associated も用意されている．この関数はポインタが結合状態であれば真，そうでなければ偽を返す．従って例えば以下のように使うことが出来る．

1if( associated(iptr) ) then
2  nullify(iptr)
3end if
4
5allocate(iptr)
6iptr = 1
7
8deallocate(iptr)

10.4.2. ポインタ配列

ポインタ配列はターゲット配列と結合させることが出来る．ただし両者の次元は同じでなければならない．ポインタ配列は配列全体を指したり，部分配列を指したりすることが出来る．

 1integer :: i, j
 2integer :: lb(2), ub(2)
 3integer, pointer :: rptr(:,:)
 4integer, target :: x(9,9)
 5
 6do j = 1, 9
 7   do i = 1, 9
 8      x(i,j) = i + (j-1)*9
 9   end do
10end do
11
12! 部分配列へ結合
13rptr => x(2:4,2:6)
14
15lb = lbound(rptr) ! (/1, 1/)
16ub = ubound(rptr) ! (/3, 5/)
17
18do j = lb(2), ub(2)
19   do i = lb(1), ub(1)
20      write(*, fmt='(i7)', advance='no') rptr(i,j)
21   end do
22   write(*,*)
23end do

上の例では13行目において rptr を x の部分配列と結合させている．ポインタ変数の場合と同様に，rptr は x への別名となり，このポインタ配列に対するアクセスは x の対応する要素へのアクセスと等しくなる．

またポインタ配列に対しても allocate による無名領域への結合が出来るので，動的配列と同様に用いることも可能である [5]．

10.4.3. データ構造

これまでの例では，ポインタは複雑な割にはありがたみが少ない．実際にポインタを使う必要性は特に感じられないだろう．ポインタが特に重要となってくるのは柔軟なデータ構造を扱う場合である．実は配列もデータ構造の一つである．配列はサイズが固定で，全ての要素が同じ型のデータの集まりなので比較的簡単に扱うことが出来る．すなわち，配列の各要素はメモリ上に連続的に配置されているので，任意の要素への直接アクセス(ランダムアクセス)が可能という長所を持つ(任意の要素のアドレスが簡単に計算出来る)． その一方で，要素をある特定の位置に挿入したい場合にはそれ以降の要素を全てずらさなければならないし，サイズの変更が簡単には出来ないという短所がある．

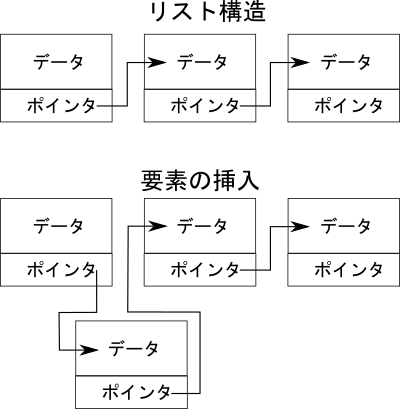
List構造．

List構造．

配列とよく対比されるデータ構造として，リスト(list)が知られている．図に示すようにリスト構造は各要素が他の要素へのポインタ(アドレス)を保持する．従って，リスト構造では任意の要素(例えば先頭から \(N\) 番目の要素)へのアクセスをしようと思ってもそのアドレスが分からない．すなわち，常に各要素に対して順番にアクセス(シーケンシャルアクセス)をしなければならない．これは配列に対するリスト構造の短所である．その一方で，任意の場所への要素の挿入や削除をするにはポインタアドレスの付け替えをするだけで実現出来る．また，リストの末尾に要素を追加するには新しい要素を生成( allocate)して，その要素に対するポインタを指定してやれば良い．このような特徴があるため，シーケンシャルアクセスしか必要とされない代わりに，頻繁にサイズ変更，要素の挿入・削除があるような用途にはリストが有用となる．

例として，各要素の値が整数であるリストは以下のように構造型を用いて定義することになる．

1type :: list_type
2   type(list_type), pointer :: next
3   integer :: value
4end type list_type

リストの実装( list.f90 )は少し長くなるのでここには掲載しないが，地道にポインタを使ってアドレスを付け替えたりするだけである．以下の例は list.f90 で実装したモジュール mod_list の使い方を示している．リストの伸長は append，要素の挿入は insert，削除は remove を用いてなどのモジュール内部手続きによって行うことが出来る．なお10行目ではモジュール内で定義した代入演算子を用いてリストを配列によって初期化している．

 1program sample
 2  use mod_list
 3  implicit none
 4
 5  type(list_type), pointer :: a
 6
 7  nullify(a)
 8
 9  write(*, fmt='(a20)', advance='no') 'initialize : '
10  a = 1
11  call show(a)
12
13  write(*, fmt='(a20)', advance='no') 'append 2 : '
14  call append(a, 2)
15  call show(a)
16
17  write(*, fmt='(a20)', advance='no') 'append 3 : '
18  call append(a, 3)
19  call show(a)
20
21  write(*, fmt='(a20)', advance='no') 'insert -1 at 1 : '
22  call insert(a, 1, -1)
23  call show(a)
24
25  write(*, fmt='(a20)', advance='no') 'insert -2 at 3 : '
26  call insert(a, 3, -2)
27  call show(a)
28
29  write(*, fmt='(a20)', advance='no') 'remove at 1 : '
30  call remove(a, 1)
31  call show(a)
32
33  write(*, fmt='(a20)', advance='no') 'remove at 3 : '
34  call remove(a, 3)
35  call show(a)
36
37  write(*, fmt='(a20)', advance='no') 'delete : '
38  call delete(a)
39  call show(a)
40
41end program sample

このプログラムの実行結果は以下のようになる．正しくリストの操作が出来ていることが分かるかと思う．

1$ ./a.out
2     initialize : List = [    1 ]
3       append 2 : List = [    1     2 ]
4       append 3 : List = [    1     2     3 ]
5 insert -1 at 1 : List = [   -1     1     2     3 ]
6 insert -2 at 3 : List = [   -1     1    -2     2     3 ]
7    remove at 1 : List = [    1    -2     2     3 ]
8    remove at 3 : List = [    1    -2     3 ]
9         delete : List = []

ここではリストの実装例を見たが，他にもキュー(queue)やスタック(stack)，ツリー(tree)，ハッシュ(hash)などがよく用いられるデータ構造の例として挙げられる．(これらはあくまでも大まかな分類であり，それぞれに対して更に細かい種類がある．例えば単にリストと言っても，片方向リストや双方向リスト，線形リストや循環リストなどの種類が存在する．)

ただし，大規模な数値計算においてこのようなデータ構造が用いられることはあまり多くない．なぜなら一般に柔軟なデータ構造を用いる処理は単純な配列に比べて効率が悪いためである．大規模数値シミュレーションではパフォーマンスが非常に重要となってくるため，複雑なデータ構造は極力使わずに実装される．しかし，配列では実装しづらい複雑なアルゴリズムを用いる必要がある場合にはデータ構造の知識も重要になってくるかもしれないので，興味のある人は勉強してみて欲しい．なおC++を始めとする多くの言語において，データ構造を扱う標準ライブラリ (組込み関数のようなもの)が存在している．従って，複雑なデータ構造の扱いが必要な場合には大人しくFortranを使うのは諦めて，他の言語を用いることを推奨する．パフォーマンスが必要な場合にはC++など，そうでないならPythonなどを使うことで開発効率が格段に向上するであろう．

10.5. デバッグのテクニック †

10.5.1. プリプロセッサ

プログラムの開発中(デバッグ中)には一時的にソースコードの一部分をコメントアウトしてその影響を調べたいことが多々あるかと思う．このような時にプリプロセッサと呼ばれる機能を用いると便利である．プリプロセッサとはC/C++のコンパイラが自動的に行う前処理のことであるが，Fortranコンパイラでも多くの場合オプションによってプリプロセッサを有効にすることが出来る．なお，プリプロセッサを使うにはgfortranであれば -cpp オプション [6] を付けてコンパイルすれば良い．または拡張子を .f90 では無く .F90 とすればオプションを指定しなくても自動的にプリプロセッサが有効になる．

プリプロセッサの機能は様々であるが，特に簡単で便利なのは以下の様な使い方である．

1#if 0
2  ここはコンパイラに無視されるので何が書いてあっても良い
3#endif

一時的に実行させたく無い処理については，上の例のように #if 0 から #endif によって囲むことでコンパイラにその部分を無視させることが出来る．コンパイラに認識させたい時には 0 を 1 に変更するだけで良いので，特定の処理が結果に与える影響を簡単に調べることが出来る．さらに

1#if 1
2  処理A
3#else
4  処理B
5#endif

としておけば，1 の時には処理A，0 の時には処理Bをそれぞれコンパイルさせる事が出来る．

プリプロセッサは基本的にC言語で用いられるものと同じなので，マクロ という機能も用いることが出来る．例えば

1#ifdef _DEBUG
2  デバッグ処理
3#endif

となっている場合に

1$ gfortran -cpp -D_DEBUG sample.f90

とすれば"デバッグ処理"がコンパイルされる．ここで -D_DEBUG は _DEBUG というマクロを定義するという意味である．マクロを用いたプリプロセッサには様々な機能があり，より複雑な指定も可能である．

1#if   _DEBUG_MODE == 0
2  デバッグモード0
3#elif _DEBUG_MODE == 1
4  デバッグモード1
5#elif _DEBUG_MODE == 2
6  デバッグモード2
7#endif

のような場合には，_DEBUG_MODE という名前のマクロの値 [7] によってコンパイルする処理を切り替えることが出来る．マクロの値もコマンドラインから明示的に与えることが出来る．例えば

1$ gfortran -cpp -D_DEBUG_MODE=1 sample.f90

のように実行すれば，マクロ _DEBUG_MODE の値が1に定義され，"デバッグモード1"の処理がコンパイルされる．

10.5.2. printfデバッグ

デバッグの基本中の基本テクニックは printf デバッグと呼ばれる．printf とはC言語で標準出力に表示するための関数名で，要するに間違っていそうな箇所に当たりをつけて，途中結果を出力して確認するという古典的な手法である．Fortranの場合にはひたすら write(*,*) で怪しい変数を出力してみれば大抵の場合(すくなくとも演習の課題レベルの場合)には自ずとバグの原因が見えてくる [8]．

このデバッグ手法はプリプロセッサと組み合わせると便利である．例えば

1#ifdef _DEBUG
2#define DEBUG_PRINT(a) write(*,*) (a)
3#else
4#define DEBUG_PRINT(a)
5#endif

としておくと，任意の場所で

1DEBUG_PRINT(出力したい変数)

のように DEBUG_PRINT というマクロを関数(サブルーチン)のように用いることが出来る．この時，コンパイル時にオプション -D_DEBUG を付けると DEBUG_PRINT の引数に与えた変数の値が出力されるが，-D_DEBUG を付けなければ何も出力されない．つまり，この形式でデバッグメッセージを埋め込んでおけば，ソースコードを一切修正することなく，コマンドラインのみでデバッグモードに切り替えることが出来る． (これは _DEBUG というマクロが定義されている場合には，DEBUG_PRINT(x) が write(*,*) (x) に変換され，それ以外の場合は単なるホワイトスペース(空白)に変換されるためである．)

このようなテクニックは非常に有用で，開発効率を大幅に高めてくれるハズなので，少しずつ身につけていくと良い．

10.5.3. gdb

To be written.

10.6. C言語とのリンク †

To be written.

10.7. Fortran 77について †

To be written.

10.8. 第10章 演習課題

参考

10.8.1. 課題1

サンプルプログラムをコンパイル・実行して動作を確認せよ．さらに，適宜修正してその実行結果を確認せよ．

10.8.2. 課題2

任意の1変数関数 \(f(x)\) およびその微分値を返す関数 \(f'(x)\) を引数として受け取り， \(f(x) = 0\) の近似解をNewton法により求めるサブルーチンを実装し，その動作を確認せよ．ただし以下の条件を満たすこと．

  • 初期値を引数として受け取る．

  • 無限ループにならないように最大の反復回数を引数として受け取る．

  • 許容誤差を引数として受け取り, 反復による近似解の変化が許容誤差以下となったら収束したとみなす．

  • 収束判定のステータスを返す．

  • 求まった近似解を返す(収束しなかった場合は最後の反復後の解の近似値)．

(二分法のモジュール bisection.f90 の mod_bisection を参考にすればよい．)

10.8.3. 課題3 †

list.f90 で定義されているリストを実装したモジュール mod_list へ以下の様な機能追加を試みよ．以下では a はリスト( type(list_type))のポインタであるとする．

  • 代入演算子が配列を受け取れるようにせよ．即ち，

1a = (/0, 1, 2/)

のようにリストに配列を代入すると元のリストを破棄し(正しく deallocate し)，与えられた配列でリストを初期化すること．

  • サンプルでは append によって単一の値をリストの終端に追加しているが，配列を与えた場合にはその各要素をリストに追加するように拡張せよ．ただしオーバーロードを用いることで，どちらも同じサブルーチン名 append で行うようにせよ．

1call append(a, 3)
2call append(a, (/4, 5/))

のようなコードが実行可能となるはずである．

  • 同様にinsertでも配列を追加できるようにせよ．

1call insert(a, 1, -1)
2call insert(a, 1, (/-3, -2/))

のようなコードが実行可能となるはずである．