5. 配列

大量のデータをまとめて扱うのに便利な配列について，その基本的な使い方や配列に関する組込み関数の使い方などを学ぼう．

参考

5.1. 基本的な使い方

配列とは 同じ型 の複数のデータを効率的に扱うために用いるデータ構造 [1] である．配列も通常の変数と同じように宣言が必要であり，宣言時には配列であることを明示的に示さなければならない．配列を宣言すると計算機の メモリ上の連続した領域 が確保され，それぞれのアドレスに添字を用いてアクセスできるようになる．

具体的には以下のように配列を宣言する．

sample1.f90 抜粋
 6  ! 最も基本的な配列の宣言
 7  integer :: a(5)
 8
 9  ! 配列の添字範囲を指定して宣言
10  integer :: b(0:4)
11  integer :: c(6:10)

7行目が最も基本的な(ここでは整数型の)配列の宣言であり，この場合は長さ5の a という名前の配列を宣言している．この例では a(1) が最初の要素であり， a(5) が最後の要素ということになる．C言語を始めとする多くの言語では配列の添字は0から始まることになっているので注意して欲しい．ただしFortranでは，10-11行目のような宣言によって宣言時に配列の添字の範囲を指定することができる．これらの例はどちらも長さ5の配列を宣言しているが， b はから0から4まで， c は6から10までが正しい配列の添字の範囲である．配列の要素にアクセスするには

sample1.f90 抜粋
17  ! doループで配列の各要素を処理する
18  do i = 1, 5
19    a(i) = i
20  enddo
21
22  do i = 0, 4
23    b(i) = i
24  enddo
25
26  ! 各要素同士の演算も出来る(添字に注意)
27  do i = 1, 5
28    c(i + 5) = 2 * a(i) + b(i - 1)
29  enddo

のように () で添字を指定すればよい．ここで， b や c は添字の範囲が異なっていることに注意しよう．

また，以下は長さ100の配列 x の総和を計算する例である．

sample1.f90 抜粋
49  ! 配列の和を求める
50  sum = 0.0_8
51  do i = 1, 100
52    sum = sum + x(i)
53  enddo

このように配列の各要素に対する処理には do ループを用いる事になる．

5.2. 配列の定数と初期化

配列は宣言する時に同時に初期化することも可能である．例えば

sample2.f90 抜粋
5  integer :: a(5) = (/1, 2, 4, 8, 16/)

のようにすればよい．ここで宣言した配列の長さと右辺の要素数は同じになっていなければならない．これを用いると parameter 属性を付けて定数配列を宣言することも出来る．

sample2.f90 抜粋
8  integer, parameter :: b(3) = (/-1, 0, 1/)

通常の定数変数と同じように，定数として宣言された配列は参照は出来るが値の変更は出来ないようになっている．

配列名を指定せずに無名の定数配列を作ることも出来る．これには"(/ "と"/)"で全体を，", "で各要素を区切って記述する．例えば以下の例では長さ3の定数配列を出力する．

sample2.f90 抜粋
11  write(*, *)(/1, 2, 3/)

5.3. 動的割付け

通常の配列はコンパイル時に静的に配列のサイズが決定される．予め必要な領域(メモリ)サイズが分かっていればこれで良いのだが，実行してみるまで必要な領域サイズが分からない場合にはこれでは対処できない．このような時には allocatable 属性を用いることで，実行時に動的に配列用にメモリを割り付けることができる．具体的には以下のように allocatable な配列を宣言すればよい．

1integer, allocatable :: x(:)

ここでは整数型の x という配列を宣言しているが，その長さはコンパイル時には不定(実行するときまで分からない)ので x(:) のように長さが指定されていないことに注意しよう．これを配列として使う前には

1allocate(x(100))

のように allocate 関数によって，メモリを割り付ける必要がある．これによって，以降は x は(この場合は長さ100の)配列として使うことができる． allocate で確保したメモリは使い終わったら

1deallocate(x)

のように deallocate で開放してやるのが作法である．いわゆるメモリリークという厄介なバグはこのような動的に割り付けたメモリの解放忘れによって発生するので気をつけよう [2]．

なお，メモリが既に割りつけられているかどうかを確認するために allocated という関数も用意されている．この関数はメモリが割り付けられている場合には真を返す．例えば

sample3.f90 抜粋
 6  ! 動的配列(実行時にしかサイズが分からない場合)
 7  integer, allocatable :: x(:)
 8
 9  ! 以下は動的(allocatable)配列の使い方
10  write(*, *) 'Input array size: '
11
12  ! 配列サイズ
13  read(*, *) n
14
15  ! allocateされていないことを確認してからallocate
16  if(.not. allocated(x)) then
17    allocate(x(n))
18  else
19    write(*, *) 'Error: already allocated'
20  endif
21
22  ! 確かにallocateされたか?
23  if(allocated(x)) then
24    write(*, *) 'Successfully allocated'
25  endif

のように使うことができる．これは標準入力から与えられた整数を長さとする配列を割り付ける例である．単に allocate するだけでなく，その前に allocated で既にメモリが割り付けられているかどうか確認している．この場合はプログラムの全体像がひと目で分かる規模のためこの確認作業は冗長であるが，場合によってはこのようなチェックが必要なこともあるだろう．

5.4. 多次元配列

ここまで扱った配列は1次元配列と呼ばれるものであったが，多次元の配列も使うことができる．分り易い例として1次元配列はベクトル，2次元配列は行列と考えればよいだろう．多次元配列の宣言には次元の分だけ(各次元の)長さを指定すれば良い．具体的には以下のような宣言となる．

sample4.f90 抜粋
 6  ! 2次元配列 (10 x 10 => 計100要素)
 7  real(8) :: a(10, 10)
 8
 9  ! 3次元配列 (4 x 8 x 16 => 計512要素)
10  real(8) :: b(4, 8, 16)
11
12  ! 動的配列も同様に宣言できる
13  real(8), allocatable :: c(:, :)
14
15  ! 動的配列: 4 x 8
16  if(.not. allocated(c)) then
17    allocate(c(4, 8))
18  endif

7行目は2次元配列，10行目は3次元配列を宣言している．このように多次元配列を宣言するには各次元の長さをカンマ区切りで指定すればよい．13行目のように多次元の動的配列も宣言することができるが，次元だけはあらかじめ指定しなければならないので c(:,:) のように次元の数だけ : をカンマ区切りで指定する．多次元の動的配列にメモリを割り付けるには17行目のように allocate の際に次元の数だけ長さを指定する必要がある．（このように多次元配列の次元数はコンパイル時に決定され，実行時には変更できない．）

宣言した配列には，次元の数だけ添字を指定して各要素にアクセスすればよい．例えば

sample4.f90 抜粋
21  do j = 1, 8
22    do i = 1, 4
23      c(i, j) = i * j
24    enddo
25  enddo

のような形である．

なお配列の次元数をrank(次元)，各次元の要素数の組をshape(形状)，全要素数をsize(サイズ)などと呼ぶことが一般的である．これらの言葉の意味は次の表を見てもらえばすぐに理解出来るであろう．

配列宣言の例

配列宣言

rank (次元)

shape (形状)

size (サイズ)

a(10)

1

(10,)

10

b(2, 5)

2

(2, 5)

10

c(10,10,10)

3

(10,10,10)

1000

d(0:9,0:99)

2

(10, 100)

1000

5.5. 配列の入出力

配列データの入出力についてもこれまでと同様に各要素を read(*,*) や write(*,*) に対する入出力リストとして与える方法もあるが，例えば配列全体を入出力リストとして与えることなども出来る．詳細は ファイル入出力 で説明するが，ここではとりあえずアスキー形式(人間の目で読める形式)のことだけを考えることにする．

5.5.1. 入力

配列の読み込みには少し注意が必要である．

sample5.f90 抜粋
 7  integer :: i
 8  real(8) :: x(10), y(10), z(10)
 9
10  ! doループで全要素を順に読み込む
11  ! この場合は改行があっても構わない
12  read(*, *) x
13
14  ! このように書いても動作は同じ
15  read(*, *)(y(i), i=1, 10)
16
17  ! よく理解していない場合にはこの形式は使わない方がよい
18  ! 1行に一つの要素が書かれている場合の読み込みはこれでよい
19  do i = 1, 10
20    read(*, *) z(i)
21  enddo

これは標準入力から3つの長さ10の配列 x, y, z のデータを読み込む例である．ここで与えるデータの改行の扱いに注意が必要である．ここでは入力として， sample5.dat をリダイレクトを用いて

1$ ./a.out < sample5.dat

のように与えることを想定している．

12行目の read は以下のsample5.datの1行目のデータを全て読み込む．ここで改行や空白，カンマ，タブなどはFortranが自動的に無視して，数値だけを読み込んでいることに注意しよう．

sample5.dat 抜粋
11.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0

15行目の read は以下のsample5.datの3-12行目のデータを全て読み込む．

sample5.dat 抜粋
 30.1
 40.2
 50.3
 60.4
 70.5
 80.6
 90.7
100.8
110.9
121.0

最後に19-21行目の do ループ中の read は

sample5.dat 抜粋
141.1
151.2
161.3
171.4
181.5
191.6
201.7
211.8
221.9
232.0

を読み込んでいる．ここで注意しなければならないのは19-21行目のような do ループと read を組み合わせた読み方では

11.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0

のような改行なしの形式のデータをうまく読み込むことができない，ということである [3]．

あまり細かいことを考えたくない人は特に理由がない限りは sample5.f90 の12行目，もしくは15行目のように 一文で配列データを全て読む ( do ループは使わない)ようにするのが無難である．

5.5.2. 出力

配列の出力の仕方を見てみよう．

sample5.f90 抜粋
23  ! doループで全要素を順に出力
24  do i = 1, 10
25    write(*, *) x(i)
26  enddo
27
28  write(*, *) x                 ! 改行せずに1行に全要素を出力
29  write(*, *)(y(i), i=1, 10)    ! これも同じ
30  write(*, *)(z(i), i=1, 10, 2) ! 1つ飛ばしで出力

24-26行目のように do ループを用いて行ってもよいが，28行目や29行目のように1行で出力することもできる．違いは write を一度呼び出しするごとに改行が挿入されるという点だけである．また30行目のように1つ飛ばしで出力することも可能である．

5.5.3. 多次元配列について

多次元配列の読み込みについては少し注意が必要である．例えば以下の sample6.dat

sample6.dat
1 1.0  2.0  3.0
2 4.0  5.0  6.0
3 7.0  8.0  9.0
410.0 11.0 12.0

を2次元配列として読み込む例を考えてみよう．

sample6.f90 抜粋
 8  real(8) :: x(3, 4)
 9
10  ! 配列のメモリが連続した要素に順に読み込まれる
11  read(*, *) x

ここでもリダイレクトを用いて

1$ ./a.out < sample6.dat

のように読み込むことを想定している．11行目の read で3x4の2次元配列 x にデータを読み込んでいることが分かるであろう．

ここで，sample6.dat の 見た目 は4x3の行列のように見えるのに対して，Fortranでは3x4の2次元配列を宣言して読み込んでいることに気をつけよう．このプログラムを実行すると， x(1,1), x(2,1), x(3,1), x(1,2), ... にそれぞれ 1.0, 2.0, 3.0, 4.0, ... が代入されることになる．これは入力が先頭から順々に行われることと，Fortranの多次元配列のメモリ並びがこの順番になっているためである(メモリ並びについては Column majorとRow major 参照)．

配列の形状が何であってもかならずこの順番で読み込まれるため，例えば

1real(8) :: x(2,6)
2
3read(*,*) x

であれば，x(1,1), x(2,1), x(1,2), x(2,2), ... の順で 1.0, 2.0, 3.0, 4.0, ... が代入されてしまう．このように多次元配列の読み込みは(初心者にとっては)必ずしも意図する結果にならないことがあるので注意して欲しい．配列はあくまで規則的にデータを並べただけのものであり，数学的な行列の概念とは必ずしも一致しないのである．

なお，ここでも read 一文でデータを全て読み込まなければならないことに再度注意しよう．以下のような2重ループ

1integer :: i, j
2real(8) :: x(3,4)
3
4! 注意: これは動かない !
5do j = 1, 4
6  do i = 1, 3
7    read(*,*) x(i,j)
8  end do
9end do

では正しく読み込むことが出来ない．

5.6. 配列に関する組込み関数

Fortranにはいくつか配列に関する便利な組込み関数が用意されている．細かい使い方についてはサンプルコードや自分で実際にコードを書いてみて動作確認をしてみるのが一番の近道である．

例えば以下の例では行列とベクトルの積を計算する matmul ，およびベクトル同士の内積を計算する dot_product の使い方を示している．（ここでは a は2次元配列， b および x は1次元配列である．）

sample7.f90 抜粋
28  ! 行列aとベクトルxの積をbに代入: b_{i} = a_{i,j} * x_{j}
29  do j = 1, n
30    do i = 1, n
31      b(i) = b(i) + a(i, j) * x(j)
32    enddo
33  enddo
34
35  write(*, *) 'b = ', b
36
37  ! 組み込み関数を使用して同じ計算を行う
38  b = matmul(a, x)
39
40  write(*, *) 'b = ', b
41
42  ! ベクトル同士の内積を計算
43  inner = 0.0_8
44  do i = 1, n
45    inner = inner + b(i) * x(i)
46  enddo
47
48  write(*, *) 'inner product 1 = ', inner
49
50  ! 組み込み関数を使用して同じ計算を行う
51  inner = dot_product(b, x)
52
53  write(*, *) 'inner product 2 = ', inner

この例では29-33行目と38行目はどちらも行列とベクトルの積を求めるものである．同様に43-46行目と51行目も全く同じ処理(内積計算)を行なっている．組込み関数を用いることで非常に簡単に処理が記述できることが分かるだろう．数学関数に加えてよく使われる組み込み関数をいくつか以下の表に挙げておこう．念のために言うとこれらは必ずしも記憶して置かなければいけないものでは無く，必要になった時に自分で調べて使いこなすことが出来ればそれで良い．(例えば富田・齋藤(2011，6章)が配列に関する組み込み関数について詳しい．)

配列に関する組み込み関数の例

関数名

説明

dot_product(x, y)

ベクトル(1次元配列) x と y の内積を返す

matmul(x, y)

行列(2次元配列)同士，もしくは行列とベクトル(1次元配列)の積を返す

transpose(x)

行列(2次元配列)の転置を返す

sum(x)

配列 x の各要素の和を返す

product(x)

配列 x の各要素の積を返す

size(x)

配列 x の全要素数(サイズ)を返す

shape(x)

配列 x の形状を1次元の整数型配列として返す

reshape(x, s)

配列 x の形状を新しい形状 s に変換したものを返す

maxval(x)

配列 x の全要素の最大値を返す

minval(x)

配列 x の全要素の最小値を返す

なお reshape を使うと多次元の配列定数を初期化することが出来る．以下はその例である．

1integer, parameter :: x(2,3) = reshape((/1, 2, 3, 4, 5, 6/), (/2, 3/))

reshape の第1引数は任意の配列であり，この配列の形状を変更したものを返す．第2引数には新しい配列の形状を指定している．ここでは左辺の配列の形状が (2,3) であるので reshape の第2引数は (/2, 3/) と形状を1次元の整数配列として指定している．当然，元々の入力配列のサイズと新しい配列のサイズは同じでなければならない [4]．

5.7. 部分配列

これまでは各要素に添字を用いて例えば x(10) のような形でアクセスしていた．Fortranではこれに加えて 部分配列 という便利な機能があり，配列の複数の要素にまとめてアクセスすることが出来る．これには添字の代わりに x(lower:upper:stride) のような形式を用いる．lower，upper，stride の意味は do 変数の指定方法(決まった回数の繰り返し(do))と同じである．従って例えば

1integer :: x(10) = (/1, 2, 3, 4, 5, 6, 7, 8, 9, 10/)
2
3write(*,*) x(1:10:2) ! 1, 3, 5, 7, 9が出力される

のように書くことが出来る．lower，upper，stride などは省略することも出来，その場合は lower は配列の最初の要素，upper は最後の要素，stride は1と解釈される．ただし stride はともかく lower，upper は明示的に書いておいた方が分かりやすい．またこれらの指定に変数を使う事もできる．

5.8. 配列演算

さらに，Fortranには非常に強力な 配列演算 という機能が用意されている．例えば

sample8.f90 抜粋
11  real(8) :: a(n), b(n), c(n)

のように定義された配列 a ， b ， c に対して，以下のような処理を行なう．

sample8.f90 抜粋
26  ! 代入
27  do i = 1, n
28    b(i) = a(i)
29  enddo
30
31  ! 配列演算による代入(上のdoループと同じ)
32  b = a
33
34  write(*, *) 'b = ', b
35
36  ! 演算
37  do i = 1, n
38    c(i) = 0.5_8 * a(i) + cos(b(i))
39  enddo
40
41  ! 配列演算(上のdoループと同じ)
42  c = 0.5_8 * a + cos(b)
43
44  write(*, *) 'c = ', c

ここで，上の例の27-29行目と32行目，37-39行目と42行目はそれぞれ等価である．このようにFortranでは 配列同士の演算をあたかも通常の変数であるかのように記述することができる ．これを配列演算と呼ぶ．数学で用いるような直感的な表現が出来ることに加えて，これを用いることでかなりタイプ量を減らすことができるのが一目見て分かるだろう．タイプ量が少ないと当然無用なバグの混入を避けることができる．さらに，配列演算はコンパイラによる最適化の恩恵を受けやすいという利点がある．

部分配列と配列演算を組み合わせることも当然可能である．例えば

sample8.f90 抜粋
10  real(8) :: x(m), y(m / 2)

のように定義された配列 x ， y に対して

sample8.f90 抜粋
49  y = 2 * x(1:m:2) + 1

のような記述ができる．部分配列や配列演算の機能は多次元配列に対しても同様に使用することができるが，配列演算は 同じ形状(次元およびサイズ)の配列に対してしか行うことが出来ない ことに注意しよう．それ以外の場合には演算が定義されないのでこれは当たり前の話である．

また，数学におけるベクトルの内積やベクトルと行列の積の計算規則とは異なり，配列演算はあくまで各要素ごとの演算であるという点に注意しよう．例えば x(100) と y(100) のような2つのサイズの等しい1次元配列の積 x*y は同じサイズ100の配列となり，スカラー値を計算する内積の計算規則とは異なる．また行列 M(100,100) とベクトル x(100) の積を計算しようとして M*x と記述しても M と x は形状が異るのでエラーとなってしまう．このような場合は先に見た dot_product や matmul を使えば良い．

5.9. 補足 †

5.9.1. メモリ領域

Fortranの通常の静的配列(static array)の場合はメモリはスタック(stack)と呼ばれる領域に保持される．環境によっては(おそらく多くのLinux環境のデフォルトでは)スタックに大きなメモリ領域を保持できないようになっている．この設定は例えばsh系のシェル(bashなど)では以下のように ulimit コマンド(csh系のシェルならば limit)で確認することが出来る．

 1$ ulimit -a
 2core file size          (blocks, -c) 0
 3data seg size           (kbytes, -d) unlimited
 4file size               (blocks, -f) unlimited
 5max locked memory       (kbytes, -l) unlimited
 6max memory size         (kbytes, -m) unlimited
 7open files                      (-n) 256
 8pipe size            (512 bytes, -p) 1
 9stack size              (kbytes, -s) 8192
10cpu time               (seconds, -t) unlimited
11max user processes              (-u) 709
12virtual memory          (kbytes, -v) unlimited

上の ulimit コマンドの出力結果から，この環境ではスタック領域が8MBに制限されているので大きな静的配列を確保することが出来ないことが分かる．プログラムの実行直後に原因不明の Segmentation fault などのエラーで終了してしまう場合はスタック領域が足りずにメモリが確保出来なかったことが原因かもしれない．

どうしても静的配列を使いたい場合には ulimit コマンドで使用可能なスタック領域を増やせば良い．もしくは静的配列の使用をやめて allocatable 配列を用いるようにすればスタック領域の制限は受けない．これは allocatable 属性付きで宣言された配列のメモリは( allocate によって)ヒープ(heap)と呼ばれる別の領域にメモリが確保されるためである．なおスタックとかヒープについて必ずしも理解している必要は無いが，原因不明のエラーが発生した時にはこのことをふと思い出して欲しい．

5.9.2. Column majorとRow major

既に説明したように配列は計算機の連続したメモリ上に確保されることが保証されている．これは1次元の場合には分かりやすいが，多次元配列の場合はどうなっているのであろうか？計算機のメモリは1次元的なアドレスからなっているので，実は多次元配列であってもメモリは内部的には1次元的に連続な領域を指している．多次元配列は単にそれらを使いやすく表示したものに過ぎない．一般的にFortranでは例えば2次元配列 x(10,10) の場合は x(1,1), x(2,1), ..., x(10,1), x(1,2), x(2,2), ...のような並び，すなわち配列の一番左の添字がメモリの連続した方向となっている．これ をcolumn majorと呼ぶ．これに対してC言語などではrow majorと呼ばれるメモリ並びが採用されており一番右側の添字がメモリの連続する方向となっている(図参照)．従って，C言語で書かれたライブラリをFortranから呼び出す際(もしくはその逆)にはこの違いに注意しなければならない．

またこのことから，効率的なプログラムとするためには多次元配列のループの書き方も注意が必要である．以下の例を考えてみよう．

 1integer :: i, j
 2real(8) :: a(10,10), s
 3
 4
 5! 例1
 6s = 0.0_8
 7do j = 1, 10
 8  do i = 1, 10
 9    s = s + a(i, j)
10  end do
11end do
12
13! 例2
14s = 0.0_8
15do i = 1, 10
16  do j = 1, 10
17    s = s + a(i, j)
18  end do
19end do

この例では5-11行目(例1)と13-19行目(例2)は全く同じ処理(配列内の全要素の総和計算)を行なっているが，多重 do ループの添字の順番が異なることに注目して欲しい．例1では左側の添字 i が内側のループで走り，例2では右側の添字 j が内側のループで走っている．基本的に計算機というのは単純作業(例えば if 分岐などがないループ)を一気に，メモリの連続している方向に順番に処理するのが得意になっている．従って，この例では左側の添字が内側ループで走る例1の方が効率の良いプログラムということになる [5]．最初はそれほど気にすることは無いが，単に「動く」だけのプログラムでは無く，「良い」プログラムとなるように細かい点についても気を配れるようになって欲しい．

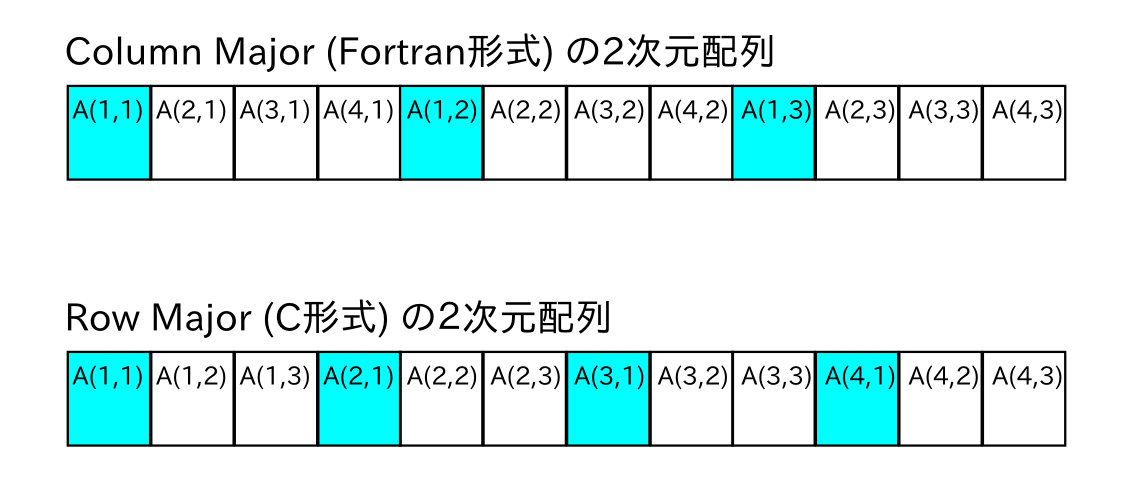
_images/storageorder.png

Column majorとRow major．メモリは左から右に連続的に並んでいる． (C言語の場合は実際には配列添字は0から始まり，添字も [] で指定することに注意．)

5.9.3. 配列境界チェック

配列の添字の範囲をはみ出した場合には何が起こるだろうか? 実はこの時何が起こるかは実行してみるまで分からない．何事も無かったかのように正常終了するように見える場合もあるし，"Segmentation fault"などのエラーが表示されて異常終了することもある．1つだけ言えることはそのようなプログラムは例え正しく動いているように見えたとしてもかなり危険な状態である．なぜならプログラムで自分が「使いたい」と要請したメモリ領域とは異なる領域へアクセスしていることになるので，自分のプログラムで用いているメモリ領域はおろか，OSがプログラムの実行に必要とする情報(コールスタックなどと呼ばれる)をも意図せず書き換えてしまうかもしれない．異常終了しなかったとしても，それはたまたま運が良かっただけなの話である．たった1行ソースコードを書き換えただけでも，プログラム中のメモリ配置が変わることで動作がおかしくなるかもしれない．(1行 write 文を入れるかどうかだけの違いで動作が変わるような場合もあるが，そういう時には大抵おかしなメモリ領域にアクセスしているものである．)

そもそも配列の添字範囲をはみ出すのは明らかなバグである．通常は効率を重視するため配列添字の境界チェックは行われないが，gfortranではコンパイル時に -fbounds-check というオプションをつけることでこの配列境界チェックを行うことが出来る．(多くのFortranコンパイラが同じようなオプションを有しているので他のコンパイラを用いる時にはチェックしてみて欲しい．) これによってもし境界をはみ出した場合にはその旨エラーが出力されてプログラムが終了する．

 1program check
 2  implicit none
 3
 4  integer :: i = 11
 5  integer :: x(10)
 6
 7  x(i) = 1
 8
 9  stop
10end program check

例えば上のソースコードをcheck.f90として保存し，コンパイル・実行した結果は以下のようになる．

1 $ gfortran -fbounds-check check.f90
2 $ ./a.out
3At line 7 of file check.f90
4Fortran runtime error: Index '11' of dimension 1 of array 'x' above upper bound of 10

配列 x の上限(10)を超えた11番目の要素にアクセスしているのでエラーが表示されているのが分かる．ただし，このようなチェックを逐一行うことで，当然実行時のパフォーマンスは犠牲になる．従って，デバッグの段階でこのような配列境界チェックを行い，時間のかかる計算を実行する際にはこのオプションは外しておこう．

5.10. 第5章 演習課題

参考

5.10.1. 課題1

サンプルプログラムをコンパイル・実行して動作を確認せよ．さらに，適宜修正してその実行結果を確認せよ．

5.10.2. 課題2

与えられた月日(例えば4月1日であれば4と1)を標準入力から読み込み，その日が1年のうちで何日目かを表示するプログラムを作成せよ．ただし閏年は無視して考えて良い．以下のような配列を用いるとよいだろう．

1integer, parameter :: days(12) = &
2     & (/31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31/)

実行結果は例えば以下のようなものになる．

1$ ./a.out
2 Input month and day :
34    # キーボード入力
41    # キーボード入力
5 day of year :           91

5.10.3. 課題3

学生のテストの点数を自動的に処理するプログラムを作成せよ．すなわち，標準入力から学生の人数および人数分のテストの点を順に読み込み，最高点，最低点，平均点，標準偏差をそれぞれ表示するプログラムを作成せよ．ただし標準偏差はデータ数 \(N\) ，各データの値 \(x_i (i=1,\ldots,N)\) ，平均値 \(\bar{x}\) を用いて

\[\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^2}\]

と定義される．

データファイル score1.dat を手元にコピーして，以下のようにリダイレクトによって作成したプログラムに読み込ませ，結果を確認せよ．実行結果は例えば以下のようなものになる．

1$ ./a.out < score1.dat
2 Best               :           98
3 Worst              :            6
4 Average            :    46.399999999999999
5 Standard deviation :    25.115201240152015

なおデータファイルには，1行目にデータ数 \(N\) ，それ以降に各データ \(x_i\) が記述されているので，まずはデータ数を読み込み配列のメモリを allocate した後に各データを読み込めば良い．( sample3.f90 を参照せよ．)

5.10.4. 課題4

標準入力から2つのベクトルを読み込み，両者の内積を計算し表示するプログラムを作成せよ． do ループを用いて地道に計算した結果と組込み関数 dot_product を用いた結果を比較すること．

以下はデータファイル vector.dat を入力とした場合の結果である．

1$ ./a.out < vector.dat
2 Inner product with do loop     :    5.4454054113084460E-017
3 Inner product with dot_product :    9.8770817913429454E-017

ただしデータは，ベクトルの長さ \(N\) ，1つ目のベクトルの要素( \(N\) 個)，2つ目のベクトルの各要素( \(N\) 個)，の順に並んでいるものとする．

5.10.5. 課題5

標準入力からベクトルと行列を読み込み，積を計算して表示するプログラムを作成せよ．これについても2重do ループを用いて地道に計算した結果と，組込み関数 matmul を用いた結果を比較すること．

以下はデータファイル matvec.dat を入力とした場合の結果である．これと同じ結果が得られることを確認せよ．

 1$ /a.out < matvec.dat
 2 Matrix-vector product with do loop
 3 -0.10000000000000001
 4 -0.89999999999999991
 5 -0.50000000000000000
 6  0.50000000000000000
 7 -1.5000000000000000
 8  1.5000000000000000
 9  1.2000000000000000
10 -2.3999999999999999
11 Matrix-vector product with matmul
12 -0.10000000000000001
13 -0.89999999999999991
14 -0.50000000000000000
15  0.50000000000000000
16 -1.5000000000000000
17  1.5000000000000000
18  1.2000000000000002
19 -2.3999999999999999

データは，ベクトルの長さ \(N\) ，ベクトルの要素( \(N\) 個)，行列の各要素( \(N^2\) 個)，が順に並んでいるものとする．また行列の要素は \(a_{11}, a_{21}, a_{31} \ldots\) の順に読み込まれることと，ベクトルと行列の積 \(b_{i} = \sum_{j} a_{i,j} x_{j}\) の添字の順番に注意せよ．

matvec.dat は以下のようなファイルになっているが，行列の部分をFortranで読み込むとあたかも転置行列を読み込んだような形になることに注意せよ．（実際に読み込んで確かめてみよ．）

 1$ cat matvec.dat
 2 8
 3
 4   0.1
 5   1.0
 6   1.0
 7   0.5
 8   0.5
 9  -1.0
10  -1.0
11   0.2
12
13  -1.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
14   1.0   -2.0    1.0    0.0    0.0    0.0    0.0    0.0
15   0.0    1.0   -2.0    1.0    0.0    0.0    0.0    0.0
16   0.0    0.0    1.0   -2.0    1.0    0.0    0.0    0.0
17   0.0    0.0    0.0    1.0   -2.0    1.0    0.0    0.0
18   0.0    0.0    0.0    0.0    1.0   -2.0    1.0    0.0
19   0.0    0.0    0.0    0.0    0.0    1.0   -2.0    1.0
20   0.0    0.0    0.0    0.0    0.0    0.0    2.0   -2.0

注釈

プログラムの入力は数学的な「ベクトル」や「行列」を読んでいる訳ではなく，単なる数値の羅列を決められた順番で読み込む．それをどのように「ベクトル」や「行列」として解釈するのかはプログラムを書く人間が決めることである．( 配列の入出力 を理解するまで熟読せよ．)

5.10.6. 課題6

標準入力から与えられた整数 \(n ( \ge 2)\) 以下の全ての素数( \(1\) は素数に含めない)を表示するプログラムを作成せよ．以下のエラトステネスのふるいと呼ばれるアルゴリズムを用いるとよい．

各整数 \(i=2,\ldots,n\) について順に

  • \(i\) が素数でなければ無視( \(i+1\) の処理へ)

  • \(i\) が素数であれば \(i\) から \(n\) の整数のうち \(i\) の倍数のものを消去(素数以外と判定)

の処理を行う．なお各整数が素数かどうかを判定するには長さ \(n\) の論理型配列を用いれば良い．この配列を全て .true. に初期化し，素数でないと判定されたものは .false. を代入して消去する．

実行結果は例えば以下のようなものになる．

 1$ ./a.out
 230                            # キーボード入力
 3 prime number :            2
 4 prime number :            3
 5 prime number :            5
 6 prime number :            7
 7 prime number :           11
 8 prime number :           13
 9 prime number :           17
10 prime number :           19
11 prime number :           23
12 prime number :           29

5.10.7. 課題7

標準入力から3つの整数 L, M, N を読み込み， 形状が (L, M, N) の整数型の3次元配列，および長さ L*M*N の整数型の1次元配列を作成せよ．その上で，

  • 組み込み関数 size, shape, lbound, ubound の引数に上記の2つの配列をそれぞれ与えた結果を出力し，その動作を確認せよ．

  • reshape を用いて1次元配列の中身を3次元配列にコピーできることを確認せよ．（ここで1次元配列に適当な値を代入してからコピーすることで reshape の動作を確認することもできる．）

 1$ ./a.out
 2 Input three positive integers (L, M, N) :
 32, 5, 7
 4 --- 3D array ---
 5 size   (should be equal to L*M*N)               :           70
 6 shape  (should be equal to 1D array (/L, M, N/) :            2           5           7
 7 lbound (should be equal to 1D array (/1, 1, 1/) :            1           1           1
 8 ubound (should be equal to 1D array (/L, M, N/) :            2           5           7
 9 --- 1D array ---
10 size   (should be equal to L*M*N)               :           70
11 shape  (should be equal to 1D array (/L*M*N/)   :           70
12 lbound (should be equal to 1D array (/1/)       :            1
13 ubound (should be equal to 1D array (/L*M*N/)   :           70

なお， L, M, N の値はそれぞれせいぜい100程度かそれ以下にしておいた方が良い．